Punkte der Ellipse bestimmen?

Question

Aufgabe:

Bestimme Sie die Punkte der Ellipse die den maximalen und den minimalen Abstand vom Koordinatenursprung haben.

ε = { (x,y) ∈ ℝ² | 3x² + 2xy + 3y² -16 = 0 } 

Problem/Ansatz:

Wie bestimmt man diese Punkte?

Comments

Ich würde davon ausgehen, dass es vier Punkte sind.

Answer 1

Hallo,

Wie bestimmt man diese Punkte?

rein rechentechnisch wohl am einfachsten mit der Methode nach Lagrange. Setzt voraus, dass Du schon mal davon gehört hast.

Haupt- und Nebenbedingung sind:$$x^2+y^2 \to \operatorname{opt}\quad \text{NB.:}\space 3x^{2} + 2xy + 3y^{2} -16 = 0$$Lagrangegleichung aufstellen und ableiten:$$L(x,\,y,\,\lambda) =x^2+y^2 + \lambda(3x^{2} + 2xy + 3y^{2} -16) \\L_x = 2x + \lambda (6x+2y) \to 0 \\ L_y = 2y + \lambda(2x + 6y) \to 0$$Und nach Elimination von $\lambda$ folgt daraus$$\begin{aligned}y(6x+2y) &= x(2x + 6y) \\ 6xy + 2y^2 &= 2x^2 + 6xy \\ y^2 &= x^2 \\\implies &6x^2 \pm 2x^2 - 16= 0 \\ \implies &(x,\,y)_{1,2} = \pm (\sqrt 2,\,\sqrt 2)\\\implies &(x,\,y)_{3,4} = \pm (2,-2)\end{aligned}$$und so sieht der Graph dazu aus:

Gruß Werner

Answer 2

Aloha :)

Du sollst die Extrema des Abstandes$$d(x;y)=\left\|\binom{x}{y}-\binom{0}{0}\right\|=\sqrt{x^2+y^2}$$unter der konstanten Nebenbedingung bestimmen:$$E(x;y)=3x^2+2xy+3y^2\stackrel!=16=\text{const}$$

Nach Lagrange muss in einem Extremum der Gradient der zu optimierenden Funktion eine Linearkombination der Gradienten aller Nebenbedingungen sein. Da hier nur eine Nebenbedingung vorliegt, ist die Situation sehr übersichtlch:$$\operatorname{grad}d(x;y)=\lambda\operatorname{grad}E(x;y)\implies\frac{1}{\sqrt{x^2+y^2}}\binom{x}{y}=\lambda\binom{6x+2y}{2x+6y}$$

Wir dividieren die 1-te Koordine durch die 2-te:$$\frac{\frac{1}{\sqrt{x^2+y^2}}x}{\frac{1}{\sqrt{x^2+y^2}}y}=\frac{\lambda(6x+2y)}{\lambda(2x+6y)}\implies\frac xy=\frac{3x+y}{x+3y}\implies\frac{x^2+3xy}{y(x+3y)}=\frac{3xy+y^2}{y(x+3y)}\implies$$$$x^2+3xy=3xy+y^2\implies x^2=y^2\implies \underline{\underline{y=\pm x}}$$

Diese Lagrange-Forderung setzen wir in die Nebenbedingung ein:$$y=x\implies 16\stackrel!=E(x;x)=8x^2\implies x=\pm\sqrt2\implies y=x=\pm\sqrt2$$$$y=-x\implies 16\stackrel!=E(x;-x)=4x^2\implies x=\pm2\implies y=-x=\mp2$$

Es gibt also 4 Punkte mit extremalem Abstand:

$$P_1(+\sqrt2;+\sqrt2)\implies d(\vec p_1)=2\implies\text{Minimum}$$$$P_2(-\sqrt2;-\sqrt2)\implies d(\vec p_2)=2\implies\text{Minimum}$$$$P_3(-2;2)\implies d(\vec p_3)=4\implies\text{Maximum}$$$$P_4(2;-2)\implies d(\vec p_4)=4\implies\text{Maximum}$$

Comments

In Polarkoordinaten :

3(r*cos φ)² + 2(r*cos φ * r*sin φ) + 3(r*sin φ)² = 16
r²*(3 + 2*cos φ * sin φ) = 16
r²  =  16 / (3 + 2*cos φ * sin φ)
dr² / dφ  =  -16 / (3 + 2*cos φ * sin φ)² * 2*(cos² φ - sin² φ)

dr² / dφ  =  0  ⇔  cos² φ = sin² φ  ⇔  cos φ * sin φ = ±1/2 
⇔  r²  =  16 / (3 ± 1)  ∈  {4 ; 8}  und  φ = kπ/4 mit k ∈ {1 ; 3 ; 5 ; 7}

---

Das ist eine gute Lösung ohne Lagrange, und sogar verständlich geschrieben.

Warum stellst du sie nicht als eigene Antwort ein?

Answer 3

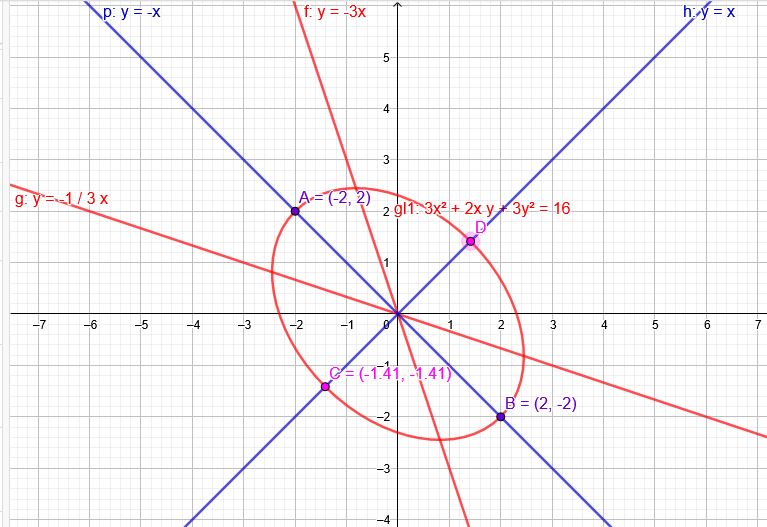
$f(x,y)=3x^2 + 2xy + 3y^2 -16$
$f_x(x,y)=6x + 2y$→ $6x+ 2y=0$ → $y=-3x$ → $m_1=-3$
$f_y(x,y)=2x+6y$→ $2x+ 6y=0$ → $y=-\frac{1}{3}x$→ $m_2=-\frac{1}{3}$
1. Winkelhalbierende:
$m_1\cdot m_2=-\frac{1}{3}\cdot(-3)=1$
$f(x)=x$
Schnitt mit $3x^2 + 2xy + 3y^2 =16$:  $8x^2 =16$ 
$x_1=\sqrt{2}$     →$y_1=\sqrt{2}$     Koordinate:   $D(\sqrt{2}|\sqrt{2})$

$x_2=-\sqrt{2}$   →$y_2=-\sqrt{2}$    Koordinate: $C(-\sqrt{2}|-\sqrt{2})$

Die Punkte C und D haben Minimalabstand vom Ursprung.

Die Nebenachse hat eine Länge von  $l_1=\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}=\sqrt{4}=2$

2.) Winkelhalbierende steht senkrecht auf der  1. Winkelhalbierenden:

$f(x)=-x$

Schnitt mit $3 \cdot x^2 + 2x y + 3 y^2 =16$:

$3 \cdot x^2 + 2x \cdot (-x) + 3\cdot (-x)^2 =16$

$3 \cdot x^2 -2x^2+ 3\cdot x^2 =16$  → $4x^2=16$

$x_1=2$    →$y_1=-2$   Koordinate: $B(2|-2)$

$x_2=-2$  →$y_2=2$   Koordinate: $A(-2|2)$

Die Punkte A und B haben Maximalabstand vom Ursprung.

Die Hauptachse hat eine Länge von $l_2=\sqrt{(-2)^2+2^2}=\sqrt{8}=2\sqrt{2}$

Diese Ellipse ist um $135°$ aus der Hauptlage heraus gedreht worden, wobei $l_1<l_2$ ist.