Ich habe so gemacht,aber suche eine Regel?

Question

Aufgabe:

Ich habe so gemacht?

Text erkannt:

10192837465
987654321

gibt es dazu eine Regel wie ich dieser Summe möglichst groß ist , wenn ja wie denn?

Text erkannt:

13. Beispiel: Die Zahlen von 1 bis 10 werden (zufällig) so angeordnet:
\( 1,3,4,6,7,2,5,8,10,9 \)
\( \begin{array}{lllllllll}2 & 1 & 2 & 1 & 5 & 3 & 3 & 2 & 1\end{array} \)
Die Unterschiede zwischen zwei benachbarten Zahlen werden daruntergeschrieben (rot). Die Summe der roten Zahlen ist \( 20 . \) Aufgabe: Ordne die Zahlen von 1 bis 10 so an, dass die Summe aller Unterschiede zweier in deiner Anordnung benachbarter Zahlen so groß wie möglich ist.

Comments

Ich vermute du studierst Informatik. Dann bietet es sich an, ein Computerprogramm zu schreiben, dass die Lösung findet.

Answer 1

Eine größere Summe der Abstände ergibt sich, wenn du die 10 mit der 6 tauschst.

Comments

habe nicht versatanden, gibt es eine Regel? Wie komme ich zum grössen Summe?

---

habe nicht verstanden

Was gibt es an

Eine größere Summe der Abstände ergibt sich, wenn du die 10 mit der 6 tauschst.

nicht zu verstehen? Schreibe deine bisherige Anordnung der Zahlen auf. Es bleibt fast alles, wie du es hattest. Nur dort, wo bei dir die 10 stand, sollst du die 6 hinsetzen. Und wo deine 6 war, sollst du die 10 hinschreiben.

---

Die Frage wäre, ob es eine Regel gibt, mit der man eine optimale Anordnung bei gegebenen Zahlen findet.

---

Diese Regel gibt es sicher. Aber dann wäre die Aufgabe sinnlos, wenn man sie gleich mitliefert. Hier ist die Möglichkeit des entdeckenden Lernens.

---

Zahri Ameer fragte ja, ob es so eine Regel gibt.

Wäre schon interessant.

---

Zuerst eine Frage ab abakus: also du meint der Sinn deiser Aufgabe ,dass man ausprobiert, ausprobiere usw...? Bis man die Lösung findet? Ich dachte so macht keinen Sinn, weil Menschen versuchen immer Regel zu finden, dit dem man schell etwas finden, und wenn ich ausprobiere, wie kann ich wissen , ob ich jetzt diesen Versuch ist der größte? Deswegen dachte ich , und immer denke , lieber mit Regel machen, denn ist sicher ich habe die größte Summe gefunden und auch schneller. Weil ich habe am Anfang versucht und habe mich gefragt, wie viel Möglichkeiten gibt und sagte muss VIEL versuchen,deswegen sagte ich suche eine Regel,aber wie soll ich wissen,dass ich satt (6) die ( 10 ) schreibe und dann bekomme die größte Summe>49 statt 45 , wie soll ich wissen?

Answer 2

Hallo Zahri,

gibt es dazu eine Regel wie ich dieser Summe möglichst groß ist

Das ist eine gute Frage. Mathematik bedeutet, sich genau darüber Gedanken zu machen! Und zwar selbst; d.h. nicht nach der Regel im Internet suchen, sondern selber überlegen, wie man zu einer möglichst großen Summe kommt.

Hier eine Hilfestellung: gesucht ist die größte Summe von DIfferenzen von Zahlen. Gegeben sind aber nur die Zahlen - in diesem Fall die 10 Zahlen von \(0\) bis \(9\). Es würde sich aber nichts an dem Problem ändern, wenn man statt dessen die 10 Zahlen von \(15\) bis \(24\) auswählt. Warum?

Nur die Differenzen sind entscheident, also sollte man diese 'sichtbar' machen. Dazu male ich Punkte, die mit einer Strecke verbunden sind. Ich habe das für 5 Zahlen gemacht. Wenn man gleich mit 10 Zahlen anfängt, wäre das zu unübersichtlich.

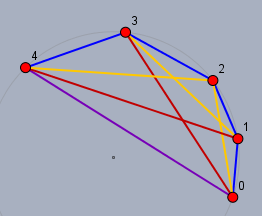
Jeder Punkt (also Zahl) ist mit jedem anderen Punkt durch eine bunte Strecke verbunden. Die Farbe der Strecke gibt die Differenz dieser beiden Zahlen an. So steht jede blaue Strecke für eine \(1\), die orange für eine \(2\), eine rote für eine \(3\) und die lila Strecke für eine \(4\).

Stelle Dir jetzt einen Käfer vor, der in einem der Punkte beginnt und so über alle Strecken krabbelt, dass er jeden Punkt genau einmal besucht. Würde der Käfer im Punkt \(0\) beginnen und über die 4 blauen Strecken zum Punkt \(4\) krabbeln, so würde er einen Weg der 'Länge' \(4\) zurück legen. Das ist nicht viel!

Beginnt er z.B. im Punkt \(3\), krabbelt zu \(0\), dann zu \(4\), dann \(1\) und \(2\), so wäre die Reihenfolge und die Summe des Weges$$\begin{array}{c}3&& 0&& 4&& 1&& 2\\ & 3&+&4&+&3&+&1&& =11\end{array}$$Das ist schon viel besser.

Nochmal ein Bild - diesmal mit 6 Zahlen

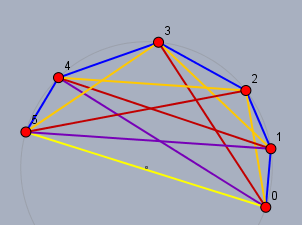
links im Bild ist der Punkt mit der Zahl \(5\) hinzu gekommen. Die gelbe Strecke steht für die Differenz \(5\). Mathematik bedeutet nun, Fragen zu finden und diese zu beantworten. Hier ein paar Beispiele:

Wievele Strecken legt der Käfer auf seinem Weg zurück?

Wieviele Strecken der 'Länge' (also Differenz) \(5\) und \(4\), usw. gibt es?

Wieviele Strecken maximal auf dem Weg des Käfers 'berühren' einen Punkt?

Wenn die gelbe und beide lilane Strecken auf dem Weg des Käfers liegen, kann er dann noch über eine rote krabbeln?

Wie verändert sich der Weg, wenn man zwei benachbarte Punkte auf dem Weg vertauscht? Also wenn der Weg \(0\space2\space4\space1\space5\space3\) ist, was bedeutet ein Vertauschen von z.B. \(1\) und \(5\) auf dem Bild: \(0\space2\space4\space{\color{red}5\space1}\space3\)?

Viel Erfolg beim Knobeln!

Gruß Werner

Comments

mit deime Beispiel  Werner-Salomon habe ich nicht ganz verstanden und die Aufgabe wird immer schwierigere. Ich meine auch mit diesem Netzt muss ich auch ausprobieren und ausprobieren, also ich sehe nichts Neues. Also zusammenfassen git es eine regel ,w eiich diese größte Summe finden? und woher weißt du, dass ich die (10) und ( 6 ) tausche ( Abakus)?

---

mit deinem Beispiel Werner-Salomon habe ich nicht ganz verstanden und die Aufgabe wird immer schwieriger

das hatte ich schon befürchtet - Schade!

Leider schreibst Du nicht (wie so viele!) was Du nicht verstanden hast.

Ich meine auch mit diesem Netzt muss ich auch ausprobieren und ausprobieren, also ich sehe nichts Neues

Probieren ist gut, um ein Gefühl für das Problem zu entwickeln. Aber ich wollte Dich dazu auffordern, Fragen zu stellen (s.o.) und Antworten darauf zu suchen.

Also zusammenfassen gibt es eine Regel ,wie ich diese größte Summe finden?

Das weiß ich nicht, aber das ist auch nicht notwendig! Es reicht doch hin eine Regel zu finden, die ein gutes Ergebnis liefert. Zu beweisen, dass diese Regel die größte mögliche Summe ergibt, ist wahrscheinlich ziemlich schwierig!

Ich habe mir Fragen (s. meine Antwort) zu den Bildern oben gestellt und diese für mich beantwortet. Und mit diesen Antworten komme ich zu folgender Regel:

Beginne mit der kleinsten und größten Zahl und setze sie neben einander in die Mitte$$\begin{array}{c}\cancel{1}&&2&&3&&4&&5&&6&&7&&8&&9&&\cancel{10}\\ && && && &&1&&10\\ \end{array}$$Dann wähle von den übrigen wieder die kleinste und die größte Zahl und setze sie neben die beiden anderen, so dass die kleine Zahl bei der großen und die größere Zahl bei der kleinen steht$$\begin{array}{c}\cancel{1}&&\cancel{2}&&3&&4&&5&&6&&7&&8&&\cancel{9}&&\cancel{10}\\ && && &&9&&1&&10&&2\\ \end{array}$$und nochmal das gleiche$$\begin{array}{c}\cancel{1}&&\cancel{2}&&\cancel{3}&&4&&5&&6&&7&&\cancel{8}&&\cancel{9}&&\cancel{10}\\ && && 3 &&9&&1&&10&&2&&8\\ \end{array}$$usw. bis in der ersten Zeile keine Zahlen mehr übrig sind. Dann erhält man$$\begin{array}{c}5&&7 && 3 &&9&&1&&10&&2&&8&&4&&6\\ &2&+&4&+&6&+&8 &+&9&+&8&+&6 &+&4 &+&2&& = 49\end{array}$$Die Summe ist nicht größer als die aus der Reihe, die Du bereits kennst, aber auch nicht kleiner ;-)

Gruß Werner

---

ich habe deine Methode( Werner-Salomon) gut verstanden, aber wie bist man ( du) dazu überhaupt gekommen?

---

... aber wie bist man ( du) dazu überhaupt gekommen?

Intuition. Ich bin mir bewußt geworden, dass die Zahlen von \(1\) bis \(10\) selbst nicht wichtig sind. Es sind nur ihre Differenzen wichtig. Und die wollte ich irgendwie darstellen. Nun gibt es aber bei 10 Zahlen 55 Zahlenpaare, von denen sich Differenzen bilden lassen. Daher habe ich mit weniger Zahlen begonnen - einmal mit 5 und dann mit 6 Zahlen.

Dann lag es nahe, für jedes Paar eine Verbindung zu zeichnen, also eine Strecke zwischen den Zahlen. Jede Strecke steht für eine Differenz zweier Zahlen. Jetzt kann man also die Differenzen 'sehen'.

Und wenn man das gemacht hat, was bedeutet es dann, die Zahlen in eine Reihe zu stellen? Es bedeutet, dass man bei irgendeiner Zahl (einem Punkt - z.B. \(3\)) anfängt und dann über eine Strecke zur nächsten geht usw. - so wie hier

Gibt: 3, 0, 4, 1, 2. Und dann habe ich mir überlegt, wie man den Weg wählen muss, um möglichst viele von den 'langen' Strecken (also den großen Differenzen) mit zu nehmen.

---

@Werner-Salomon:

Coole Idee!

---

Zitat((Intuition. Ich bin mir bewußt geworden, dass die Zahlen von \(1\) bis \(10\) selbst nicht wichtig sind. Es sind nur ihre Differenzen wichtig. Und die wollte ich irgendwie darstellen. Nun gibt es aber bei 10 Zahlen 55 Zahlenpaare, von denen sich Differenzen bilden lassen. Daher habe ich mit weniger Zahlen begonnen - einmal mit 5 und dann mit 6 Zahlen.Dann lag es nahe, für jedes Paar eine Verbindung zu zeichnen, also eine Strecke zwischen den Zahlen. Jede Strecke steht für eine Differenz zweier Zahlen. Jetzt kann man also die Differenzen 'sehen'.Und wenn man das gemacht hat, was bedeutet es dann, die Zahlen in eine Reihe zu stellen? Es bedeutet, dass man bei irgendeiner Zahl (einem Punkt - z.B. \(3\)) anfängt und dann über eine Strecke zur nächsten geht usw. - so wie hier)))---> wieder habe nicht ganz verstanden.

Aber ich denke ich kann mir diese besser merken:ALso 1 und 10 und 2 und 9 dann 3 und 8 usw, dann kommt 49. Ich werde nicht mehr Zeit für diese Aufgabe investieren: Dieser Regle denke, ich reicht

---

gibt es dazu eine Regel wie ich dieser Summe möglichst groß ist

um diese Frage abschließend zu beantworten:

Wenn es 10 beliebige Zahlen wären, so wäre das Problem meiner Meinung nach identisch mit dem des Handlungsreisenden. Und für dieses Problem ist keine geschlossene Lösung (Regel) bekannt.

Ich habe ein Programm geschrieben, welches alle 1814400 Möglichkeiten durchprobiert. Und die maximal zu erreichende Summe ist \(49\) und die wird von 576 unterschiedlichen Zahlenreihen errreicht. Die 'gespiegelten' nicht mitgerechnet!

Answer 3

Ich versuche es zuerst mit drei Zahlen.

1 2 3 → 1+1=2

1 3 2 → 2+1=3

3 1 2 → 2+1=3

Nun vier Zahlen.

1 2 3 4 → 1+1+1=3

4 1 3 2 → 3+2+1=6

Kann das Ergebnis größer als 6 sein?

Die größte Differenz ist 4-1=3. Sie gibt es nur einmal. Damit die Summe größer als 6 ist, müsste man 3+2+2=7 rechnen.

2 4 1 3 → 2+3+2=7 ✓ Mehr geht nicht.

...

Bei 10 Zahlen würde ich gucken, welche Differenzen wie oft vorkommen, und daraus die Reihenfolge zusammen basteln.

10-1=9 einmal,

10-2=9-1=8 zweimal,

7 dreimal

...

1 neunmal.

Nun brauchen wir neun möglichst hohe Differenzen.

Optimal wäre

9+8+8+7+7+7+6+6+6=64

Mehr geht auf keinen Fall.

Fangen wir mal an:

8 2 10 1 9 3 → 6+8+9+8+6=37

Nun noch 4, 5, 6 und 7 hinzufügen.

6 4 8 2 10 1 9 3 7 5

 → 2+4+6+8+9+8+6+4+2=49

Gibt es eine Regel?

Wenn man die Anzahl der Zahlen n nennt und die maximale Summe der Differenzen s(n) erhält man folgende Werte:

n	2	3	4	5	6	7	8	9	10
s(n)	1	3	7	11	17	23	31	39	49

Für gerade Werte von n erkennt man, dass die Differenz der s(n)-Werte systematisch zunimmt.

1+6 → 7+10 → 17+14 → 31+18 → 49+...

Für ungerade n:

3+8 → 11+12 → 23+16 → 39+...

Die Differenz nimmt also immer um 4 zu.

Damit kann man eine Formel herleiten, wenn man möchte.

n gerade: ½n²-1

n ungerade: ½(n²-1)-1

:-)

Comments

Da ich die Aufgabe interessant finde, habe ich meine Antwort ergänzt.

:-)

---

Damit kann man eine Formel herleiten, wenn man möchte.

Ja kann man! zwei Beispiele:$$s(n) = \left\lfloor\frac12 n^2\right\rfloor - 1 = \frac14\left(2n^2 + (-1)^n-5\right)\\s(n) = \left\lfloor(n-1)^{\sqrt{\pi}}\right\rfloor$$liefern beide die selben Ergebnisse bis \(n=11\), ab da geht es dann auseinander ;-)

siehe hier.