Hallo zusammen, es geht um das Thema Portfoliorisiko. Ich habe 2 Formeln gegeben und verstehe nicht genau wann welche verwendet wird.
Text erkannt:
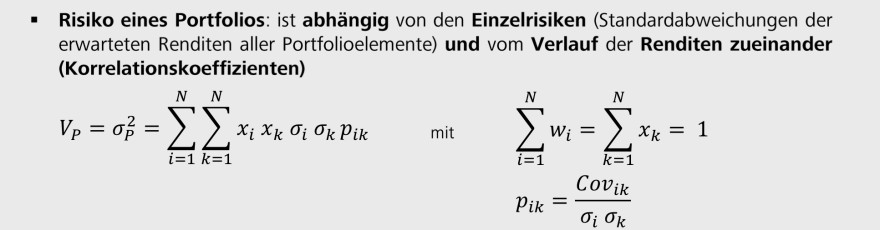
- Risiko eines Portfolios: ist abhängig von den Einzelrisiken (Standardabweichungen der erwarteten Renditen aller Portfolioelemente) und vom Verlauf der Renditen zueinander (Korrelationskoeffizienten)
\( \begin{aligned} V_{P}=\sigma_{P}^{2}=\sum \limits_{i=1}^{N} \sum \limits_{k=1}^{N} x_{i} x_{k} \sigma_{i} \sigma_{k} p_{i k} \quad \text { mit } \quad & \sum \limits_{i=1}^{N} w_{i}=\sum \limits_{k=1}^{N} x_{k}=1 \\ & p_{i k}=\frac{\operatorname{Cov}_{i k}}{\sigma_{i} \sigma_{k}} \end{aligned} \)

Text erkannt:
Ermittlung des Minimum-Varianz-Portfolios (MVP)
\( \sigma_{\mathrm{p}}^{2}=\mathrm{x}^{2} \cdot \sigma_{1}^{2}+(1-\mathrm{x})^{2} \cdot \sigma_{2}^{2}+2 \cdot \mathrm{x}(1-\mathrm{x}) \cdot \sigma_{1} \cdot \sigma_{2} \cdot \rho_{1,2} \)
2. Minimierung der Zielfunktion und Auflösung nach \( \mathrm{x} \) :
\( \frac{\mathrm{d} \sigma_{\mathrm{p}}^{2}}{\mathrm{dx}}=2 \cdot \mathrm{x} \cdot \sigma_{1}^{2}+2 \cdot(1-\mathrm{x}) \cdot(-1) \cdot \sigma_{2}^{2}+2 \cdot(1-\mathrm{x}) \cdot \mathrm{COV}_{1,2}-2 \cdot \mathrm{x} \cdot \mathrm{COV}_{1,2}=0 \)
\( x^{*}=\frac{\sigma_{2}^{2}-\operatorname{COV}_{1,2}}{\sigma_{1}^{2}+\sigma_{2}^{2}-2 \cdot \operatorname{COV}_{1,2}} \)
Aufgabe:
Text erkannt:
2 Asset Fall (60\% Aktien / \( 40 \% \) Anleihen)
a) Bestimmen Sie den erwarteten Return und die entsprechende Standardabweichung des aktuellen Portfolios (60\% Aktien / \( \mathbf{4 0 \%} \) Anleihen).
Portfoliorendite:
\( \begin{array}{l} R_{P}=E\left(r_{i}\right)=\mu \quad R_{P}=\sum \limits_{i=1}^{N}\left(x_{i} * E\left(r_{i}\right)\right) \\ R_{P}=0,60 * 0,10+0,40 * 0,06=\mathbf{8}, \mathbf{4 0} \% \end{array} \)
Portfoliorisiko:
\( \begin{array}{l} \sigma_{P}^{2}=x^{2} \sigma_{1}^{2}+(1-x)^{2} \sigma_{2}^{2}+2 x(1-x) \sigma_{1} \sigma_{2} \rho_{1,2} \quad \text { (Zielfunktion von Folie 51) } \\ \sigma_{P}^{2}=0,6^{2} * 0,15^{2}+0,4^{2} * 0,08^{2}+2 * 0,6 * 0,4 * 0,15 * 0,08 * 0,3=0,0109 \\ \sigma_{P}=\sqrt{0,0109}=\mathbf{1 0}, \mathbf{4 4} \% \end{array} \)

Text erkannt:
3 Asset Fall (55\% Aktien / 35\% Anleihen / 10\% Immobilien)
b) Bestimmen Sie nun den erwarteten Return und die entsprechende Standardabweichung des modifizierten Portfolios bestehend aus 55\% Aktien, 35\% Anleihen und \( 10 \% \) Immobilien.
Portfoliorendite: \( \quad R_{P_{R E}}=0,55 * 0,10+0,35 * 0,06+0,10 * 0,07=\mathbf{8}, \mathbf{3 0} \% \)
Portfoliorisiko:
\( \sigma_{P}^{2}=x_{1}^{2} \sigma_{1}^{2}+x_{2}^{2} \sigma_{2}^{2}+x_{3}^{2} \sigma_{3}^{2}+2 * x_{1} x_{2} * \sigma_{1} \sigma_{2} * \rho_{1,2}+2 * x_{1} x_{3} * \sigma_{1} \sigma_{3} * \rho_{1,3} \)
\( +2 * x_{2} x_{3} * \sigma_{2} \sigma_{3} * \rho_{2,3} \)
\( \sigma_{P_{R E}}^{2}=0,55^{2} * 0,15^{2}+0,35^{2} * 0,08^{2}+0,10^{2} * 0,10^{2}+2 * 0,55 * 0,35 * 0,15 * \)
\( 0,08 * 0,3+2 * 0,55 * 0,1 * 0,15 * 0,1 * 0,25+2 * 0,35 * 0,1 * 0,08 * \)
\( 0,1 * 0,15=0,0095 \)
Problem/Ansatz:
Die MVP Formel scheint auch nur für 2 Anlagen im Portfolio zu gelten.
Warum wird die Zielfunktion hier in a) verwendet, obwohl wir die optimale Gewichtung nicht errechnen?
In b) wird die erste Formel zum Risiko verwendet, wenn ich das richtig sehe?
Vielen Dank im Voraus und liebe Grüße!