Flächeninhalte Dreieck

Question

Aufgabe:

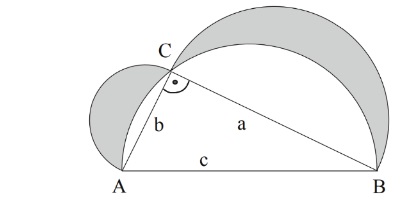
Gegeben ist ein rechtwinkliges Dreieck ABC. Über a ist der Halbkreis Ha,
über b der Halbkreis Hb und über c der Halbkreis Hc gezeichnet.

Zeigen Sie, dass die Summe der Flächeninhalte der beiden grauen Flächen
so groß ist wie der Flächeninhalt des rechtwinkligen Dreiecks.

Problem/Ansatz:

Ich kann mir vorstellen, dass es mit dem Satz des Pythagoras beweisbar ist, aber nicht wie.

Liebe Grüße!

Answer 1

Hallo,

Die Fläche \(F\) der beiden grauen Sicheln ist die Summe aus den beiden Halbkreisen über \(a\) und \(b\) plus der Fläche \(F_{\triangle}\)  des Dreiecks minus der Halbkreis über \(c\) - also:$$F = \frac12\left(\frac{a}{2}\right)^2 \pi + \frac12\left(\frac{b}{2}\right)^2 \pi + F_{\triangle} - \frac12\left(\frac{c}{2}\right)^2 \pi\\ \phantom{F} = \frac12\underbrace{(a^2+b^2-c^2)}_{=0}\frac{\pi}{4} + F_{\triangle} \\ \phantom{F}= F_{\triangle}$$nennt sich Möndchen des Hippokrates.

Gruß Werner