Aloha :)
Um eine komplexe Zahl \(z\in\mathbb C\) als Punkt in der Gauß'schen Zahlenebene darzustellen, wird der Realteil auf der \(x\)-Achse und der Imaginärteil auf der \(y\)-Achse eingetragen. Wir zerlegen daher die Zahlen \(z\in\mathbb C\) in Real- und Imaginärteil:$$\pink{z=x+i\cdot y}\quad;\quad x;y\in\mathbb R$$
Wir müssen in dieser Aufgabe die Definitionsbereiche für \(x\) und \(y\) einschränken, damit der Punkt in der Menge \(M\) liegt. Die erste Forderung lautet \((z'\cdot z\le4)\). Das bedeutet:$$z'\cdot z=(x+iy)'\cdot(x+iy)=(x-iy)\cdot(x+iy)=x^2-(iy)^2=\pink{x^2+y^2\stackrel{!}{\le}4}$$
Die zweite Forderung, die ebenfalls erfüllt sein muss, lautet \((\,|z+1|\ge1\,)\). Das bedeutet:$$|z+1|=|(x+iy)+1|=|(x+1)+iy|=\sqrt{(x+1)^2+y^2}\ge1\implies\pink{(x+1)^2+y^2\ge1}$$
Die erste Bedingung \((\pink{x^2+y^2\le4})\) sagt, dass die Punkte \((x;y)\) innerhalb eines Kreises mit Radius \(2\) um den Ursprung herum liegen müssen. Der Rand des Kreises gehört dazu.
Die zweite Bedinung \((\pink{(x+1)^2+y^2\ge1})\) beschreibt alle Punkt \((x;y)\), die außerhalb eines Kreises mit Mittelpunkt \((-1|0)\) und Radius \(1\) liegen. Der Rand dieses Kreises erfüllt bereits die Bedingung.
Wir haben also einen großen Kreis mit Radius \(2\) um den Ursprung, aus dem ein kleiner Kreis mit Radius \(1\) um den Punkt \((-1|0)\) herausgetrennt wurde.
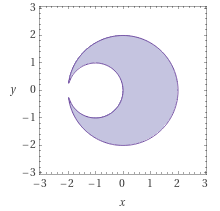
Der große Kreis ist links geschlossen, das kommt in der Zeichnung nicht raus, weil die Strichdicke zu klein ist. Beide Ränder, sowohl der des Außenkreises als auch der des Innenkreises gehören zu der Menge \(M\) dazu.