Welche Auslenkung hat der Massepunkt zum Zeitpunkt t = 3π/2? / Ingenieurmathematik

Question

Aufgabe:

Ein an einer Feder aufgehängter Massepunkt wird ab dem Zeitpunkt t = 0 einer periodisch
wirkenden äußeren Kraft F unterworfen, die zu einer Auslenkung führt. Die Lage y(t) des
Massepunktes zum Zeitpunkt t >_ 0 (größer gleich) kann als Lösung des Anfangswertproblems
y'' (t) + 9y(t) = F * sin(2t), y(0) = y' (0) = 0 beschrieben werden.

Welche Auslenkung hat der Massepunkt zum Zeitpunkt t = 3π/2 ?

Problem/Ansatz:

Hallo kann mit bitte jemand bei dieser Aufgabe helfen.

Vielen Dank vorab!

Answer 1

Hallo,

y'' (t) + 9y(t) = F * sin(2t), y(0) = y' (0) = 0

homogene Gleichung:

y'' (t) + 9y(t) =0

Ansatz: y=e^( k t) , 2 Mal ableiten und in die DGL einsetzen

->Charakt. Gleichung:

k^2+9=0

k_1,2= ± 3i

y_h= C₁ cos(3t) +C₂ sin(3t)

Ansatz yp:

yp= A cos(2t) +B sin(2t)

y_p 2 Mal ableiten, Koeffizientenvergleich

y=y_h +y_p

dann in das Ergebnis die AWB einsetzen

darin wieder t = 3π/2

-----------------------------------------

kompletter Weg:

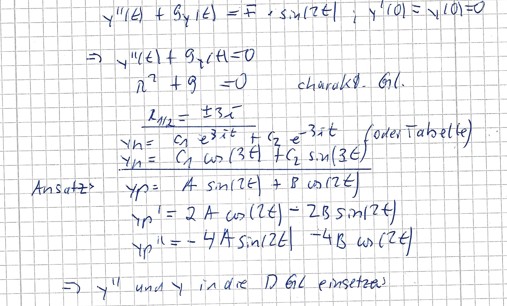
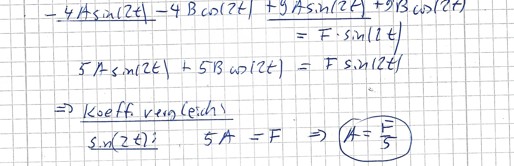
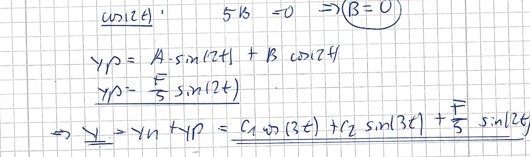
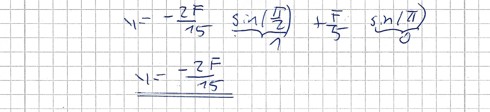
falls Du eine Tabelle benutzen darfst: (betreffs homogene Lösung siehe oben )

siehe hier:

https://micbaum.y0w.de/uploads/LoesungsansaetzeDGLzweiterOrdnung.pdf

Blatt 2; Punkt 1 , 3. Fall

Comments

Vielen Dank! :)

---

Hat jemand ein letztes Ergebnis zum Vergleichen, ich habe y(3pi/2)=(F/5)*sin(3pi/2).

Ich freue mich auf euere Antworten, Liebe Grüße

---

Ich habe erhalten:

C₁=0

C₂= \( \frac{-2F}{15} \)

und damit:

y((3π)/2)= \( \frac{-2F}{15} \)

Wenn Du weitere Fragen frag ruhig :)

---

Danke für deine Antwort. wie hast du quasi die linke Seite mit der rechten in Verbindung gebracht? Weil bei mir ist y´(0)= -3C1*sin(0)+3C2*cos(0) und ich habe da nichts mit der Kraft in Verbindung gebracht, denn in meinem Ansatz ist das ja die homogene Lösung also die linke Seite, wobei ich ja die rechte Seite komplett außer acht lasse oder?

LG

---

Du mußt die Anfangsbedingung einsetzen in:

von der Lösung y  mußt Du die 1.Ableitung bilden

---

Nochmals Danke! Ich sehe jedoch die Verbindung zwischen den linken und rechten Teil der Gleichung noch nicht....:( Hast du zufällig den kompletten Rechenweg zu Hand, dass ich mal bei meiner Lösung detailliert auf Fehlersuche gehen kann? Das würde mir sehr helfen.

---

siehe oben

.................................

---

Vielen Dank für deine Hilfe. Das hat mir wirklich sehr geholfen das Thema zu verstehen.