max-academy.de/contentPlayer/5f00d9d4af792d0067e07a9c/5f00dfc0af792d0067e07aa3
das ist der Link zur folgenden Aufgabe, bei der ich der Berechnung der 2. Ableitung nicht verstehe.
Text erkannt:
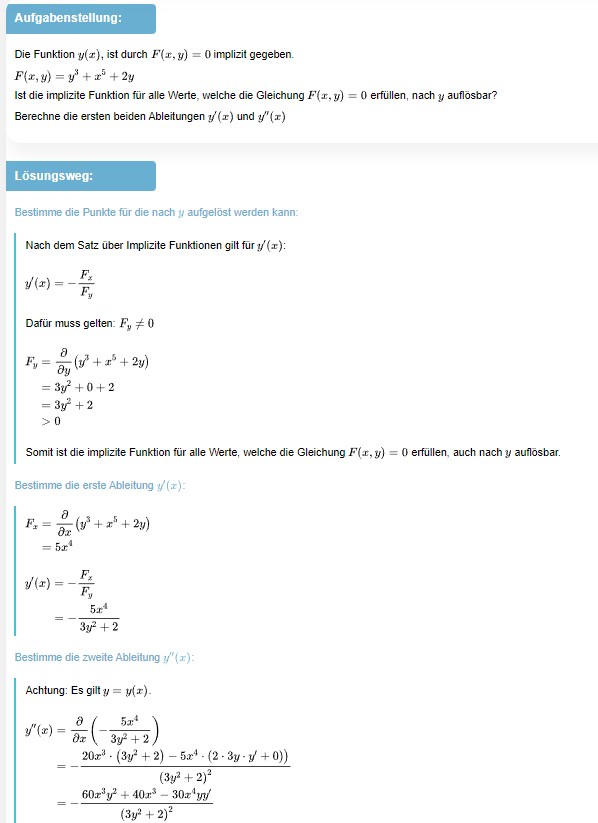
Aufgabenstellung:
Die Funktion \( y(x) \), ist durch \( F(x, y)=0 \) implizit gegeben.
\( F(x, y)=y^{3}+x^{5}+2 y \)
Ist die implizite Funktion für alle Werte, welche die Gleichung \( F(x, y)=0 \) erfüllen, nach \( y \) auflösbar?
Berechne die ersten beiden Ableitungen \( y^{\prime}(x) \) und \( y^{\prime \prime}(x) \)
Lösungsweg:
Bestimme die Punkte für die nach \( y \) aufgelöst werden kann:
Nach dem Satz über Implizite Funktionen gilt fü \( y^{\prime}(x) \) :
\( y^{\prime}(x)=-\frac{F_{z}}{F_{y}} \)
Dafür muss gelten: \( F_{y} \neq 0 \)
\( \begin{aligned} F_{y} &=\frac{\partial}{\partial y}\left(y^{3}+x^{5}+2 y\right) \\ &=3 y^{2}+0+2 \\ &=3 y^{2}+2 \\ &>0 \end{aligned} \)
Somit ist die implizite Funktion für alle Werte, welche die Gleichung \( F(x, y)=0 \) erfüllen, auch nach \( y \) auflösbar.
Bestimme die erste Ableitung \( y^{\prime}(x) \) :
\( \begin{aligned} F_{x} &=\frac{\partial}{\partial x}\left(y^{3}+x^{5}+\right.\\ &=5 x^{4} \\ y /(x) &=-\frac{F_{x}}{F_{y}} \\ &=-\frac{5 x^{4}}{3 y^{2}+2} \end{aligned} \)
Bestimme die zweite Ableitung \( y^{\prime \prime}(x) \) :
Achtung: Es gilt \( y=y(x) \).
\( \begin{aligned} y^{\prime \prime}(x) &=\frac{\partial}{\partial x}\left(-\frac{5 x^{4}}{3 y^{2}+2}\right) \\ &=-\frac{\left.20 x^{3} \cdot\left(3 y^{2}+2\right)-5 x^{4} \cdot\left(2 \cdot 3 y \cdot y^{\prime}+0\right)\right)}{\left(3 y^{2}+2\right)^{2}} \\ &=-\frac{60 x^{3} y^{2}+40 x^{3}-30 x^{4} y y^{\prime}}{\left(3 y^{2}+2\right)^{2}} \end{aligned} \)
Ich habe hier alles verstanden bis auf, wie man hier auf y''(x) gekommen ist, daher würde mich eine Erklärung sehr freuen, vielen Dank :)