Aufgabe:
Bildung der Inversen einer Verteilungsfunktion (hier die Errorfunktion)…:
Problem/Ansatz:
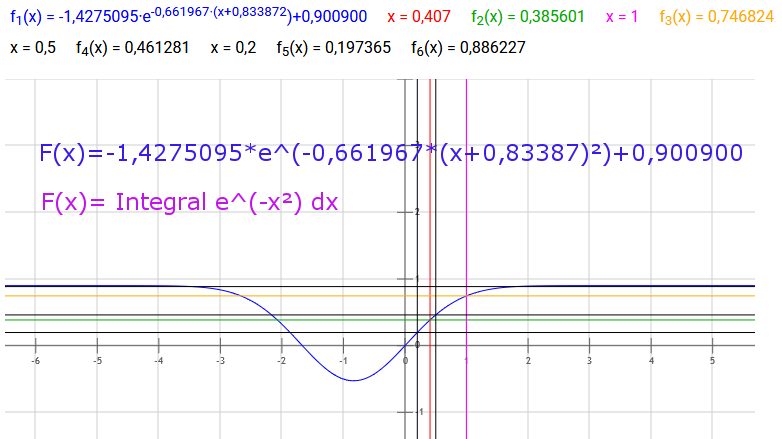
Die ist die von mir angenäherte / relativ genau ermittelte Errorfunktion...., habe e^(-x^2) nur "gespiegelt" an der x-Achse und die Konstanten iterativ durch 4 Wertepaare ermittelt! Bilde ich jetzt die Inverse dieser Verteilungsfunktion, was dann möglich ist, erhalte ich dann eine Streuungsfunktion? Dies wäre unter anderem für die Ausbreitung von Licht wichtig..., wenn dieses auch eine andere Verteilungsfunktion hat, bzw. eine andere Dichtefunktion! Die Inverse ist doch immer das Gegenteil der Ausgangsfunktion, oder?
habe die Graphen noch einmal extra dargestellt, mit der Inversen.....:
~plot~ ((188992836237300000*x+157595456353197351)*e^(-(661967*(x+83387/100000)^2)/1000000))/100000000000000000;e^(-x^2);-1.4275095*e^(-0.661967*(x+0.83387)^2)+0.900900;(32469*sqrt(10305700000000000000000000-22389600000000000000000000*ln(-(19330383*(x-9009/10000))/17414755)))/125000000000000000-83387/100000;x; ~plot~
Danke für die "reine" Beurteilung dieser Frage, bzw. deren Bewertung! (habe früher mal, es ist sehr lange her, Statistik in der Mathematikausbildung während des Studiums gehabt....., ich bitte um Ihr Verständnis!)
Viele Grüße, Bert Wichmann!