Aufgabe: Berechne die Höhe des Dreiecks
Text erkannt:
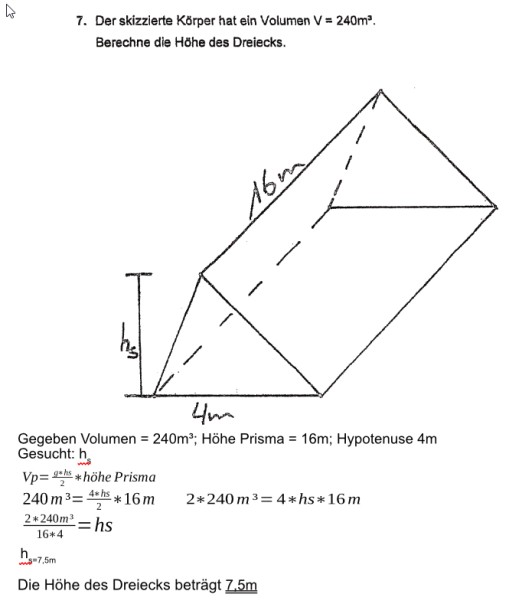
7. Der skizzierte Körper hat ein Volumen \( V=240 \mathrm{~m}^{2} \). Berechne die Höhe des Dreiecks.
Gegeben Volumen \( =240 \mathrm{~m}^{3} \); Höhe Prisma \( =16 \mathrm{~m} ; \) Hypotenuse \( 4 \mathrm{~m} \) Gesucht: \( h_{s} \)
\( V p=\frac{g s h \leq}{2} * \) höhe Prisma \( 240 m^{3}=\frac{4 * h s}{2} * 16 m \quad 2 * 240 m^{3}=4 * h s * 16 m \) \( \frac{2 * 240 m^{3}}{16 * 4}=h s \)
\( \mathrm{h}_{s=7,5 \mathrm{~m}} \)
Die Höhe des Dreiecks beträgt \( 7.5 \mathrm{~m} \)
Problem/Ansatz:
Hallo Leute, ich habe versucht folgende Aufgabe zu lösen, meine Frage ist, ob mein Lösungsansatz richtig ist?