Wie rechnet man die Wendestellen und Sattelstellen der Funktion f(x)=1/3 x^3 - x^2 + x -1 aus?

Question

Gegeben ist die Funktion f(x)=1/3x³-x²+x-1

Die Extremstellen sind bei x₁=1, x₂=1

Wie kann man die Wendestellen und Sattelstellen dieser Funktion ausrechnen?

Answer 1

f(x) = 1/3 x^3 - x^2 + x - 1

f'(x) = x^2 - 2x + 1

f''(x) = 2x - 2

Für die Wendestelle setzt man die 2. Ableitung gleich Null

f''(x) = 0

2x - 2 = 0

x = 1

Damit ist die Wendestelle gleichzeitig die Extremstelle. Dann ist es eine Sattelstelle. Auf die hinreichende Bedingung kann verzichtet werden wenn ein Funktionsgraph vorliegt.

Comments

Muss man nicht Sattelpunkt ausrechnen, indem man WP in die Funktion einsetzt?

---

Ja. wenn Du den Sattelpunkt ausrechnen willst brauchst Du noch die y-Koordinate 

f(1) = - 2/3

=> Sattelpunkt bei SP(1 | -2/3)

Du sprachst in der Aufgabe nur von Wendestellen und Sattelstellen. Und das wäre nur die x-Koordinate.

 

Answer 2

Für Wendestellen gilt die notwendige Bedingung:
f''(x) = 0:

 

f''(x) = 2x - 2

Es liegt also eine mögliche Wendestelle bei x = 1 vor.

Nun muss die hinreichende Bedingung überprüft werden:
f''(x) = 0 und f'''(x) ≠ 0:

f'''(x) = 2 ⇒ f'''(1) = 2 ≠ 0, also liegt ein Wendepunkt vor.

 

Unter einem Sattelpunkt versteht man einen Wendepunkt mit waagerechter Tangente, also einen Wendepunkt, der zusätzlich f'(x) = 0 erfüllt.

Alle möglichen Wendestellen kennen wir bereits, nur bei x=1 liegt eine. Also muss dort die 1. Ableitung überprüft werden:

f'(x) = x² - 2x + 1

f'(1) = 0 ⇒ es handelt sich sogar um einen Sattelpunkt!

(Daraus folgt übrigens auch, dass es sich bei deinen berechneten Extremstellen nicht um echte Extremstellen handelt, sondern nur um stationäre Stellen, die in Wirklichkeit Sattelstellen sind.)

Comments

f(x) = 1/3 x^3 - x^2 + x - 1

f'(x) = x^2 - 2x + 1

f''(x) = 2x - 2

Bedingung für Wendestelle: f''(x)=0

1.) f''(x) = 0                2.) f'''(x)= 2                                            

    2x - 2 = 0                    f'''(x)= 2 ≠0

    x = 1                           f'(1) ≠0       Also liegt ein WP vor

                                                       

 

Wie groß ist die Steigung bei x=1

f'(1)=1*1²-2*1+1

f'(x)=0            WP bei dem die Steigung gleich 0 ist, liegt ein Sattelpunkt vor

 

f(1)= -0,666666  =-2/3

(1/-2/3)  liegt Sattelpunkt vor

 

Muss ich bei der Berechnung der Wendestellen nicht schreiben das der WP bei (1/-2/3)  liegt??

---

Wie der Mathecoach schon gesagt hat, hast du nur nach Wende-/Sattelstellen gefragt, deswegen habe ich auch nur die Stellen ausgerechnet.

Wenn explizit nach Punkten gefragt ist, müssen natürlich auch die Funktionswerte ausgerechnet werden.

 

Falls das für Verwirrung sorgt:
Punkt = (Stelle, Wert)

P = (x, f(x))

Answer 3

Gegeben ist die Funktion f(x)=1/3x³-x²+x-1

Das ist ein Polynom 3. Grades. Wenn lokale Extrema existieren, gibt es genau einen Hochpunkt und einen Tiefpunkt. Und aus Symmetriegründen genau in der Mitte zwischen diesen beiden liegt die Wendestelle der Kurve.

 

f ' (x) = x² - 2x + 1   = (x-1)²       | Hat die Nullstellen x₁ = x₂ = 1 Das ist eine Stelle mit horizontaler Tangente. Könnte eine Extremalstelle sein, muss aber nicht! Hier fallen der Hochpunkt und der Tiefpunkt zusammen, deshalb liegt ein Sattelpunkt vor.

(x-1)²  ist nie kleiner als 0. Die Kurve verläuft monoton steigend. Keine Möglichkeit für ein lokales Maximum oder Minimum.

 

f ' ' (x) = 2x - 2 = 0                    |Bedingung für Wendestelle f ' ' = 0

2(x-1)=0

x_w = 1                       Wendestelle x_W = 1

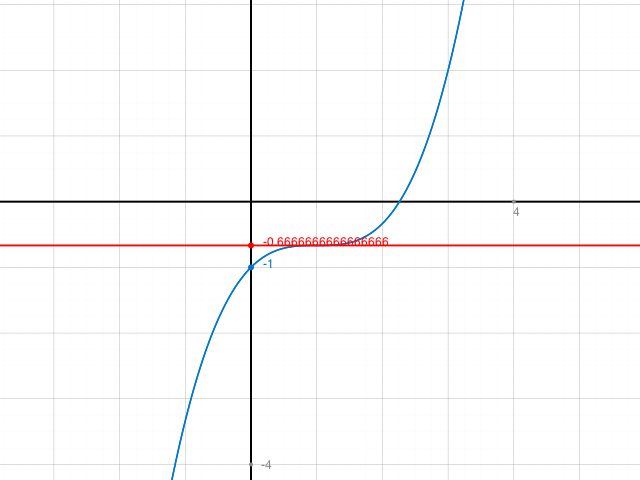
In der Skizze sieht man, wie das hier aussieht:

P(1 ;   -2/3) ist der Terrassenpunkt ( Sattelpunkt)    

Horizontale Tangente aber kein Vorzeichenwechsel bei der Steigung.