berechnen Sie nun approximativ mit Hilfe des Zentralen Grenzwertsatzes die Wahrscheinlichkeit

Question

Aufgabe:

Sie erheben in einem Elektrogroßmarkt die Anzahl der verkauften neuen Fernsehgeräte pro Tag. Sei \( X \) die Anzahl der verkauften Fernseher pro Tag, dann ergibt sich folgende Verteilung für \( X \) :

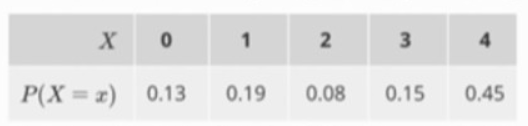
Zur Lageroptimierung berechnen Sie nun approximativ mit Hilfe des Zentralen Grenzwertsatzes die Wahrscheinlichkeit, dass innerhalb von 300 Tagen mehr als 761 Fernseher verkauft werden unter der Annahme, dass die Verkäufe einzelner Tage voneinander unabhängig sind. (Geben Sie die Lösung bitte in Prozent an!)

Problem/Ansatz:

Mit R:

T<- (0.13+0.19+0.08+0.15+0.45)/5
E<- (T*300)
Var<- sqrt(E)

und nun weiß ich nicht mehr weiter ich glaube auch der Ansatz ist falssch, kann mir bitte jemand helfen?

Answer 1

Bei einer diskreten Zufallsvariablen gilt


\(\displaystyle E[X]=\mu=\sum \limits_{i=1}^{n} x_{i} \cdot p\left(X=x_{i}\right) \)


\(\displaystyle V[X]={\sigma}^{2}=\sum \limits_{i=1}^{n}\left(x_{i}-E[X]\right)^{2} \cdot p\left(X=x_{i}\right) \)


Damit kann man eine Normalverteilung berechnen.

Comments

Eine Normalverteilung mit μ = 2,6 und σ² = 2,5592 (exakt) der Anzahl TV pro Tag ergibt bei 300 Tagen eine Normalverteilung mit μ = 780 und σ² = 230328, d.h. eine Standardabweichung von etwa 480.

761 verkaufte TV sind etwa 0,04 Standardabweichungen unter dem Erwartungswert.

Damit und mit der Standardnormalverteilungstabelle komme ich auf eine Wahrscheinlichkeit von etwa 51,6 %.