lineare Gleichungen und Koordinatensystem

Question

Aufgabe:

a) Bestimme die Gleichung der Geraden \( \mathrm{g}_{1} \).

b) Zeichne den Graphen \( g_{2} \) der Gleichung \( y=-1.25 x+5 \)

c) Zeichne die Gerade \( g_{3} \) zu dieser Tabelle, finde die Gleichung und ergänze die Tabelle.

d) Bestimme den Schnittpunkt von \( \mathrm{g}_{1} \) und \( \mathrm{g}_{3} \).

Problem/Ansatz:

Wie geht aufgabe b) & wie löse ich bei der aufgabe c) die anderen in der tabelle

Comments

zu c)

zwei Punkte sind gegeben, nämlich (-2|-6,5) und (3|6). Nur zur Erinnerung: der erste Wert in den Klammern ist der x-Wert, der zweite der y-Wert. Hier ändert sich der x-Wert um 5, nämlich von -2 nach +3 und der y-Wert um 12,5. Das bedeutet, dass für jede Änderung von x um 1 sich der y-Wert um 2,5 ändert. Rechnung: 12,5:5=2,5.

Damit haben wir die Steigung der Funktion: 2,5. Wenn wir das in die allgemeine Funktionsgleichung "y=mx+n" einsetzen, ergibt sich für den ersten Punkt: -6,5=2,5*(-2)+n. Daraus ergibt sich n=-1,5. Die Funktion ist y=2,5x-1,5

für x=0 ist y=-1,5

für x=18 ist y=43,5

für y=72,25 ist x=29,5

Answer 1

zu b)

die 5 ist der Schnittpunkt mit der y-Achse, die -1,25 ist die Steigung, das bedeutet, wenn sich x um den Wert 1 ändert, ändert sich y um den Wert -1,25. Der Wert ist negativ, also gilt für jedes x das 1 größer wird, wird y um 1,25 kleiner.

Antwort zu c) folgt

Answer 2

Willkommen in der Mathelounge!

b) Zeichne den Schnittpunkt mit der y-Achse ein. Gehe von dort 2 Einheiten nach rechts und 2,5 Einheiten nach unten. Zeichne diesen Punkt und verbinde beide. Du kannst natürlich auch eine Einheit nach rechts und 1,25 nach unten gehen, aber so geht es wahrscheinlicher einfacher.

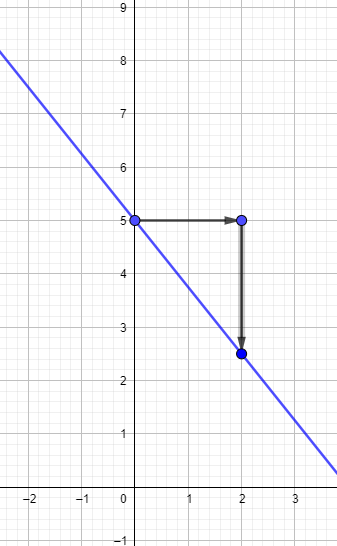
c) Zeichne die bekannten Punkte in ein Koordinatensystem.

Um von A nach B zu gelangen, gehst du 5 Einheiten nach links und 12,5 nach oben. Somit ist die Steigung m = 2,5. Die y-Achse wird bei -1,5 geschnitten. Also lautet die Gleichung der Geraden g₃

y = 2,5x - 1,5

Alternativ berechnest du die Steigung mit der Formel \(m=\frac{y_1-y_2}{x_1-x_2}\ und setzt dann die Koordinaten eines Punktes ein, um den Schnittpunkt mit der y-Achse zu bestimmen.

Um die y-Koordinate an der Stelle x = 18 zu bestimmen, setzt du 18 für x in die Gleichung ein und rechnest aus.

Um die x-Koordinate für den Funktionswert 72,25 zu bestimmen, setzt du 2,5x - 1,5 = 72,25 und löst nach x auf.

Du kannst dich gerne melden, wenn noch etwas unklar ist.

Gruß, Silvia

Comments

Um den Schnittpunkt zu bestimmen, setzt du beide Geradengleichungen gleich und löst nach x auf.

0,8x - 2 = 2,5x - 1,5

Setze dein Ergebnis in eine der beiden Gleichung ein, um die y-Koordinate des Schnittpunktes zu bestimmen.

---

Danke für die Erklärung!

Habe jedoch noch eine frage: Ich weiss nicht ganz wie ich auf y=2.5 - 1.5 komme. Ich habe zuerst die koordinaten aufgeschrieben: x= -2/6.5 & y=3/6 dann habe ich die x werte minus gerecht und dann auch die y werte das gibt es ja dann den bruch 12.5/5 das gibt 2.5. Aber wie komme ich auf die 1.5?

(ah und wir benutzen die formel y=ax+b)

Dankeschön!!!!

---

y = ax + b

a = 2,5

Jetzt die Koordinaten eines Punktes für x und y einsetzen. Ich nehme (3|6).

\(6=2,5\cdot 3 +b\\ 6=7,5+b\\ -1,5 = b\)

---

Danke Hab es verstanden! :)