Geraden verschieben und spiegeln

Question

Löse diese Aufgabe rechnerisch. Eine Konstruktion dazu kann dir aber helfen. Gegeben sind die beiden Geraden g1: y = 0.4x-3 und g2: y = -2x + 2 Bestimme die Gerade g₁ ', die gegenüber g₁ um 4 Einheiten nach oben ver schoben ist. Spiegle die Gerade g2 am Punkt Z (2/2), das ergibt die Gerade g2'. Bestimme jetzt den Schnittpunkt der Geraden g₁ 'und 92'

Answer 1

Mache das doch zunächst zeichnerisch. Geogebra könnte dir dabei helfen.

Sag uns vielleicht auch, wo konkret die Schwierigkeiten liegen. Weißt du wie sich die Funktionsgleichung ändert, wenn man eine Gerade um 4 Einheiten nach oben verschiebt?

Weißt du evtl. auch, wie sich eine Funktionsgleichung ändert, wenn man eine Gerade an einem Punkt spiegelt? Beachte dabei, dass du ja nur zwei Punkte der Geraden spiegeln musst.

Answer 2

Hallo,

du kannst g1 leicht nach oben verschieben, indem du den Schnittpunkt mit der y-Achse um vier Einheiten nach oben verlegst. Die Steigung der Gerade bleibt gleich.

g2: Zeichne die Gerade und den Punkt Z. Suche dir markante Punkte auf g2 und bedenke, dass die Spiegelpunkte den gleichen Abstand von Z haben.

Zum Beispiel Punkt A. Der hat den senkrechten Abstand zu Z von einer Längeneinheit. Damit haben A und A' einen Abstand von 2 Längeneinheiten. Nun kannst du einen weiteren Punkt auf der Spiegelgeraden bestimmen, indem du zu der y-Koordinate eines Punktes 2 addierst, und die Funktionsgleichung aufstellen.

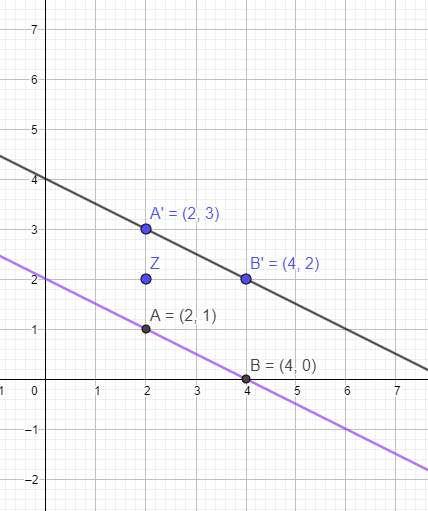
Den Schnittpunkt bestimmst du durch Gleichsetzen g₁' = g₂'.

Gruß Silvia