Berechne die Entfernung x zum Turm und seine Höhe h (Trigonometrie)

Question

Aufgabe:

Man kann die Entfernung x zu einem Turm mithilfe des höhen Winkelmessers bestimmen. Man wählt Zwei Messpunkte A und B in einer Linie mit dem Fusspunkt des Turms. Anschließend misst man von beiden Punkten aus den Höhenwinkel zur Spitze des Objekts und die Entfernung der Punkte A und B. Berechne die Entfernung x zum Turm und seine Höhe h

Problem/Ansatz:

Wir haben heute diese Aufgabe im Unterricht bearbeitet, nur leider habe ich den Lösungsweg nicht wirklich verstanden, vor allem den Teil indem man plötzlich mit Gleichungen / dem Gleichsetzverfahren rangeht. F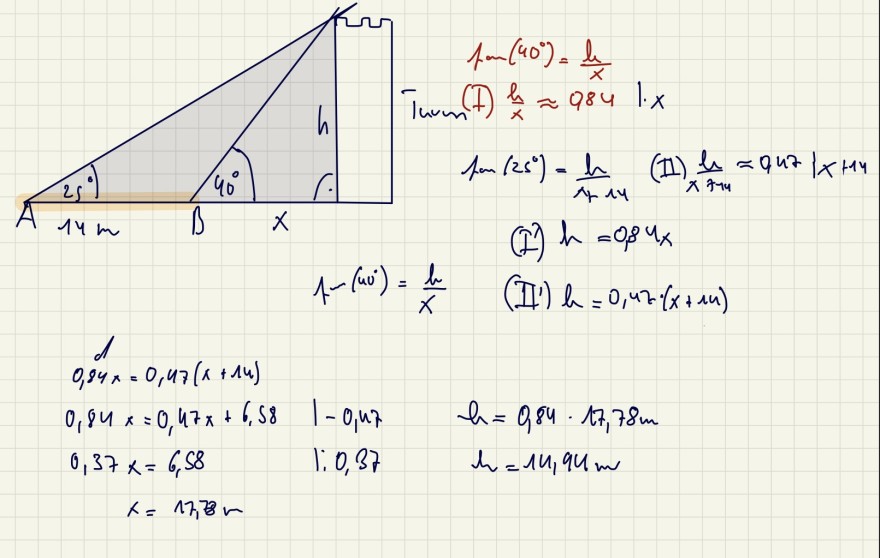

Text erkannt:

1- \( \left(40^{\circ}\right)=\frac{h}{x} \quad \) (I') \( h=0,42 \cdot(x+14) \)
\( 0,84 x=0,47(x+14) \)
\( \begin{array}{lll}0,84 x=0,47 x+6,58 & 1-0,47 & h=0,84 \cdot 17,78 m \\ 0,37 x=6,58 & 1,0,37 & h=14,94 \mathrm{~m}\end{array} \)
\( x=17,78 m \)

alls es mir Jemand erklären könnte wäre ich sehr dankbar!

Answer 1

Offensinchtlich gilt

h / x = tan(40°) = 0.8391
h / (x + 14) = tan(25°) = 0.4663

Löse jetzt das Gleichungssystem. Ich erhalte x = 17.51 m ∧ h = 14.69 m

Comments

Gleichsetzungsverfahren bedeutet beide Gleichungen zu einer Unbekannten auflösen und dann den Rest der Gleichungen gleichsetzen.

h / x = tan(40°) → h = x·tan(40°)
h / (x + 14) = tan(25°) --> h = (x + 14)·tan(25°)

Gleichsetzen

x·tan(40°) = (x + 14)·tan(25°)
x·tan(40°) = x·tan(25°) + 14·tan(25°)
x·tan(40°) - x·tan(25°) = 14·tan(25°)
x·(tan(40°) - tan(25°)) = 14·tan(25°)
x = 14·tan(25°) / (tan(40°) - tan(25°))
x = 17.5119307

Den Rest sollte man jetzt leicht schaffen.

---

Es ist ein Fehler, wenn die Lehrkraft meint zu Anfang den tan() auf 2 wesentliche Stellen runden zu müssen um später die Lösung mit 4 wesentlichen Stellen anzugeben. Das kann nicht genau werden.

Answer 2

großes rechtwinkliges Dreieck: A, F(Fußpunkt des Turmes) und S (Spitze des Turmes):

1.) \(tan (25°)=\frac{h}{14+x} \)

kleines rechtwinkliges Dreieck: B, F und S:

2.) \(tan (40°)=\frac{h}{x} \)

Auflösung von  1.) nach h:

\(h=tan (25°)*(14+x) \) Dies nun einsetzen in 2.):

\(tan (40°)=\frac{tan (25°)*(14+x)}{x} \) 

Auflösung nach x:

\(tan (40°)*x=tan (25°)*(14+x) \)

\(tan (40°)*x=14*tan (25°)+x*tan (25°) \)

\(x*tan (40°)-x*tan (25°) =14*tan (25°)\)

\(x*([tan (40°)-tan (25°)]=14*tan (25°)\)

\(x=\frac{14*tan (25°)}{[tan (40°)-tan (25°)]}=17,51\)