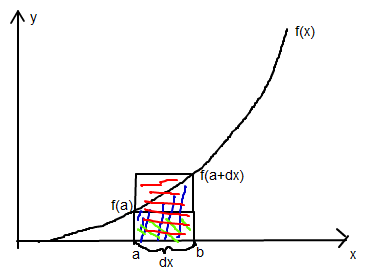
Um zu verdeutlichen warum das Integral von f(x) die Fläche unter einem Graphen beschreibt hab ich mich mal an dieser Skizze versucht..
Also, die grün schraffierte Fläche ist folgendermaßen definiert
f(a)dx
Für die blau schraffierte Fläche (die exakte Fläche unter dem Graphen) brauchen wir eine Funktion die wir noch nicht kennen.. nennen wir sie A.
Dann ist die blau schraffierte Fläche
A(b)-A(a)
Und die rote Fläche ist so definiert
f(a+dx)dx
Jetzt stellen wir eine Ungleichung auf.. Aus der Zeichnung ist klar..
f(a+dx)dx > A(b)-A(a) > f(a)dx
da dx nichts anderes ist als b-a, können wir die Ungleichung auch so schreiben
f(a+b-a)(b-a) = f(b)(b-a) > A(b)-A(a) > f(a)(b-a) |:(b-a)
f(b) > (A(b)-A(a))/(b-a) > f(a)
Wenn wir davon aber nun den Grenzwert bilden für b↦a haben wir ja nichts anderes dastehen als
f(a) > A'(a) > f(a)
Mit dem Einschließungssatz sehen wir, dass unsere gesuchte Flächenfunktion A abgeleitet unsere Funktion f sein muss.. daraus folgt, die Flächenfunktion muss f "aufgeleitet" also eine Stammfunktion von f sein..
Grüße