Aufgabe: Bei dieser Aufgabe soll die Richtungsableitung in Richtung e im Punkt (0,0) bestimmt werden.Da f nicht differenzierbar im Punkt (0,0) ist,muss man die Richtungsabletung über die Schnittfunktion bestimmmen.Mein Problem ist,dass ich nicht auf die in den Lösungen angegebene Schnittfunktion komme,wenn ich (t*1/Wurzel2,1/Wurzel2) in f einsetze.Wie muss hier umgeformt/vereinfacht werden.damit man auf die ensprechende Schnittfunktion kommt.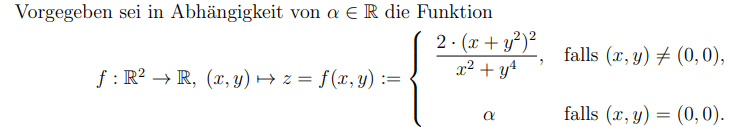
Text erkannt:
Vorgegeben sei in Abhängigkeit von \( \alpha \in \mathbb{R} \) die Funktion
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R},(x, y) \mapsto z=f(x, y):=\left\{\begin{array}{cl} \frac{2 \cdot\left(x+y^{2}\right)^{2}}{x^{2}+y^{4}}, & \text { falls }(x, y) \neq(0,0), \\ \alpha & \text { falls }(x, y)=(0,0) \end{array}\right. \)

Text erkannt:
Die Schnittfunktion von \( f \) im Punkt \( \left(x_{0}, y_{0}\right)=(0,0) \) in Richtung des Vektors \( \vec{e} \) lautet
\( h(t):=f\left(\frac{t}{\sqrt{2}}, \frac{t}{\sqrt{2}}\right)=\frac{2 \cdot(\sqrt{2}+t)^{2}}{2+t^{2}} t \in \mathbb{R} . \)
Es gilt
\( h^{\prime}(t)=2 \cdot \frac{2 \cdot(\sqrt{2}+t) \cdot\left(2+t^{2}\right)-(\sqrt{2}+t)^{2} \cdot 2 \cdot t}{\left(2+t^{2}\right)^{2}}, t \in \mathbb{R} \)
und insbesondere
\( \frac{\partial f}{\partial \vec{e}}(0,0)=h^{\prime}(0)=2 \cdot \sqrt{2} \)