E-Funktion bei Supermarkt

Question

Aufgabe:

Der Wettbewerb unter den Lebensmittelhändlern ist in Deutschland sehr gross. Um überall für Kunden erreichbar zu sein grillt eine Anzahl von 3200 Supermärktgen als optimal. Eine Supermarktketten expandiert sei dem Jahr 2000 stark. Die Anzahl der Märkte wird näherungsweis durch die Funtkion f mit f(t)= 3200-3050*E^-0,08*t modelliert. Dabei hilft t die Zeit in Jahren und t=0 entspricht dem Jahr 2000

c) Berechnen die den zweijährigen Zeitraum in dem die Supermarktketten um durchschnittlich 150 Märkte pro Jahr beträgt

d) gerechnen Sie den Zeitpunkt, zu dem die Expansionsgeschwindigkeit der Supermarktkette 100
Märkte pro Jahr betràgt.

Problem/Ansatz:

Bei c weiss muss ich ja vermutlich die 150, in f(t) einsetzten. Ich weiss leider nicht wo. Bei d habe ich genau das selbe problem.

Wäre daher nett wenn ihr mir weiter helfen könntet.

LG

Comments

Bei dieser tollen Grillparty sollte man den Exponenten in Klammern setzen. Weil sonst ist es keine E-Funktion...

\(\displaystyle 3200-3050\cdot e^{-0,08}\cdot t \quad \neq \quad 3200-3050\cdot e^{-0,08\cdot t} \)

Answer 1

c) Löse die Gleichung f(t+2) - f(t) = 150.

d) Löse die Gleichung f'(t) = 100.

Bei c weiss muss ich ja vermutlich die 150, in f(t) einsetzten

Die Gleichung

        3200-3050*E^-0,08*t = 150

besagt

        Die Anzahl der Supermärkte zum Zeitpunkt t ist 150.

Und mit

        f(150) = 3200-3050 e^-0,08·150

berechnest du die Anzahl der Supermärkte im Jahr 2150.

Comments

Erstmal danke für die schnelle Antwort. Leider verstehe ich den Lösungsansatz nicht. Wäre es möglich dass du die Lösungswege für c und d etwas genauer aufzeigst erklärst.

Beste grüsse

---

Was verstehst du an dem Lösungsansatz nicht?

---

Also wenn ich dass richtig verstehe ist das dein Lösungsansatz Ansatz

c) Löse die Gleichung f(t+2) - f(t) = 150.

d) Löse die Gleichung f'(t) = 100.

Und die darauf folgende antwort erklärt den Fehler von dem einsetzen von der 150.
Deinen Lösungsansatz für d verstehe ich und kann ich auch umsetzten, allerdings scheitert es bei mir bei c. Ich verstehe nicht was ich für bei

f(t+2) - f(t) 

einsetzten soll und wie ich es ausrechne. Muss ich 3200-3050*E^-0,08*t + 2 - 3200-3050*E^-0,08*t =150 rechnen? Was soll ich tuen?

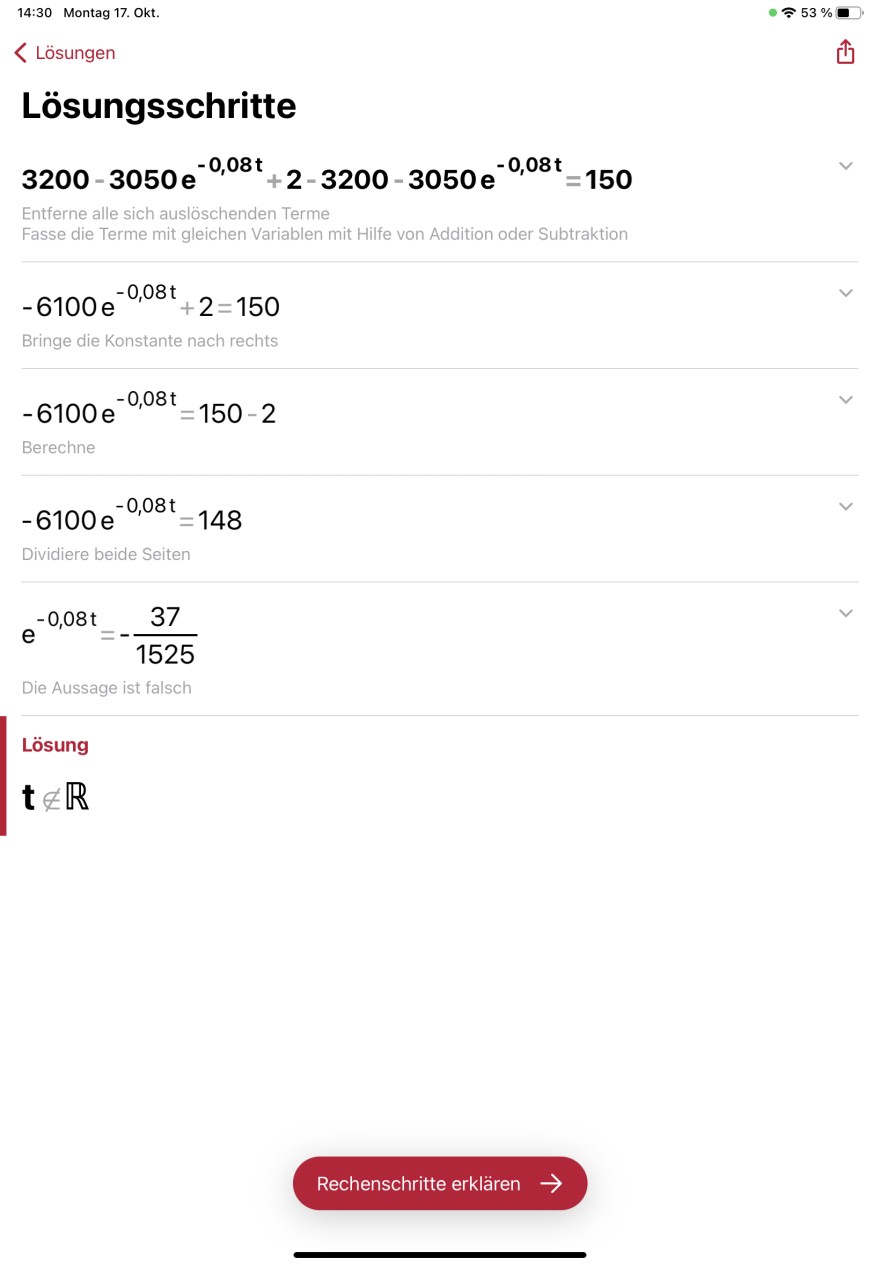
Text erkannt:

14:30 Montag 17. Okt.
< Lösungen
Lösungsschritte
\( 3200-3050 e^{-0,08 t}+2-3200-3050 e^{-0,08 t}=150 \)
Entferne alle sich auslöschenden Terme
Fasse die Terme mit gleichen Variablen mit Hilfe von Addition oder Subtraktion
\( -6100 e^{-0,08 t}+2=150 \)
Bringe die Konstante nach rechts
\( -6100 e^{-0,08 t}=150-2 \)
\( -6100 e^{-0,08 t}=148 \)
Dividiere beide Seiten
\( e^{-0,08 t}=-\frac{37}{1525} \)
Die Aussage ist falsch
Lösung
\( \mathbf{t} \notin \mathbb{R} \)
Rechenschritte erklären \( \rightarrow \)

---

f(t+2) - f(t) = 150

\((3200-3050\mathrm{e}^{-0,08(t+2)}) - (3200-3050\mathrm{e}^{-0,08t}) = 150\)

---

Achso danke. Das hilft :)