Aufgabe:
Den Dieb finden!
Problem/Ansatz:
Aufgabe A3
Es gibt drei Verdachtige fur den Raub eines Lutschers im Suwarenladen: a, b und c. Genau einer von
ihnen hat den Lutscher gestohlen. Beim Verhor sagen sie Folgendes aus:
(a) Ich war es nicht. Auerdem war ich gar nicht am Tatort.
(b) Ich war es nicht. Auer mir war auch noch c am Tatort.
(c) Ich war es nicht. Der Dieb ist a. b war nicht am Tatort.
Finden Sie unter der Annahme, dass die Unschuldigen die Wahrheit gesagt haben, den Dieb!
Soweit bin ich bis zu diesem Aussage gekommen, aber es klappt einfach nicht. 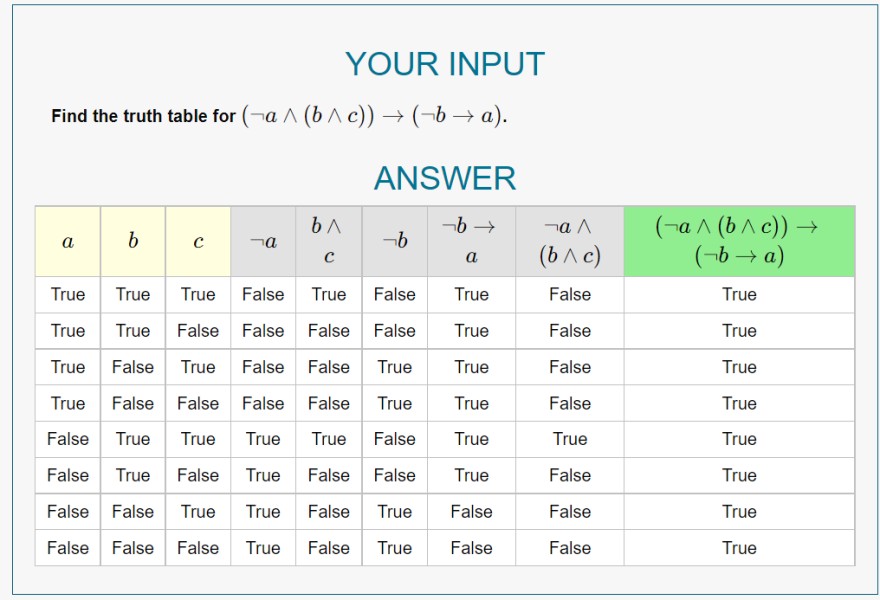
Text erkannt:
YOUR INPUT
Find the truth table for \( (\neg a \wedge(b \wedge c)) \rightarrow(\neg b \rightarrow a) \).
ANSWER
\begin{tabular}{|c|c|c|c|c|c|c|c|c|}
\hline\( a \) & \( b \) & \( c \) & \( \neg a \) & \( b \wedge \) & \( \neg b \) & \( \neg b \rightarrow \) & \( \neg a \wedge \) & \( (\neg a \wedge(b \wedge c)) \rightarrow \) \\
& & & & \( c \) & & \( a \) & \( (b \wedge c) \) & \( (\neg b \rightarrow a) \) \\
\hline True & True & True & False & True & False & True & False & True \\
\hline True & True & False & False & False & False & True & False & True \\
\hline True & False & True & False & False & True & True & False & True \\
\hline True & False & False & False & False & True & True & False & True \\
\hline False & True & True & True & True & False & True & True & True \\
\hline False & True & False & True & False & False & True & False & True \\
\hline False & False & True & True & False & True & False & False & True \\
\hline False & False & False & True & False & True & False & False & True \\
\hline
\end{tabular}