Wie viele Menschen nutzen das Internet, um Gesundheitsinformationen zu erhalten? In einer Umfrage unter 1790 zufällig ausgewählten erwachsenen australischen Internetnutzern gaben 1553 an, dass sie solche Informationen über das Internet beziehen.
a) Bewerten Sie anhand dieser Ergebnisse den Nachweis, dass mindestens 85 % der erwachsenen australischen Internetnutzer Gesundheitsinformationen aus dem Internet beziehen. Nehmen Sie α = 1 % an, verwenden Sie einen P-Wert-Ansatz und berücksichtigen Sie alle relevanten Schritte eines formalen Hypothesentests.
Was ist der P-Wert Ansatz?
Ich glaube gerade den Ansatz über den P-Wert hatte ich schon mind. 2-mal vorgemacht.
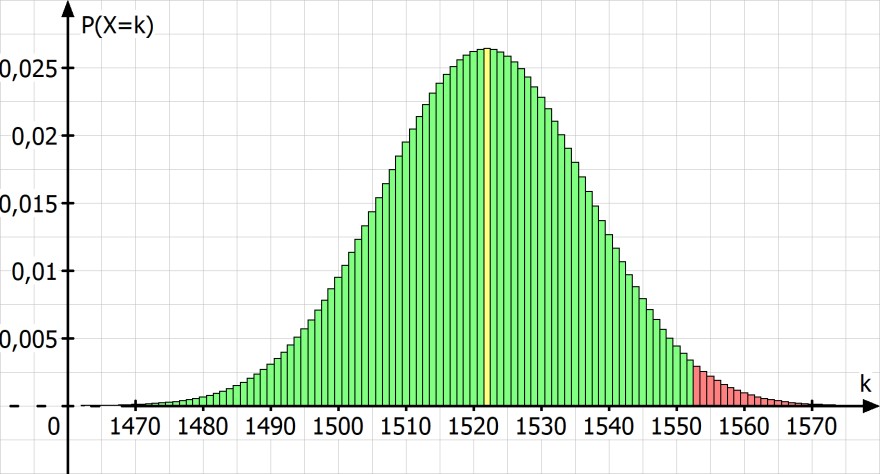
P(X ≥ 1553 | n = 1790, p = 0.85) = 1.88% > 1%
Die Nullhypothese, dass p < 0.85 ist, kann nicht abgelehnt werden. Wir können also nicht nachweisen, dass mind. 85% der erwachsenen australischen Internetnutzer Gesundheitsinformationen aus dem Internet beziehen.
Skizze