\(P(X\le4)=\phi\left(\frac{4-\mu_X}{\sigma_X}\right)=\phi(1,659812)=0,951524\approx95,15\%\)
Das es bei 95% liegt, kann gut hinhauen. Ich habe nämlich 3 mal dieses Zufallsexperiment durchgeführt und es kam jedes mal 2 raus. Das Ergebnis 2 als kumulierte Summe scheint hier also von allen Ergebnissen am wahrscheinlichsten zu sein.
Mich würde interessieren wie Sie auf den Erwartungswert von 0.08 kommen. Ich habe ihn so berechnet: Wahrscheinlichkeiten * Auszahlungen und komme auf folgenden Wert: 0.21+0.28+0.24-0.03-0.08-0.06+49*0 = 0.56.
Und als Varianz dann: 0.21(1-0.56)^2+0.14*(2-0.56)^2+0.08(3-0.56)^2+0.03(-1-0.56)^2+0.04(-2-0.56)^2+0.01(-6-0.56)^2 = 1.57
Und was mir auffällt, dass bei Normalverteilung, genau das Gegenereignis dargestellt wird: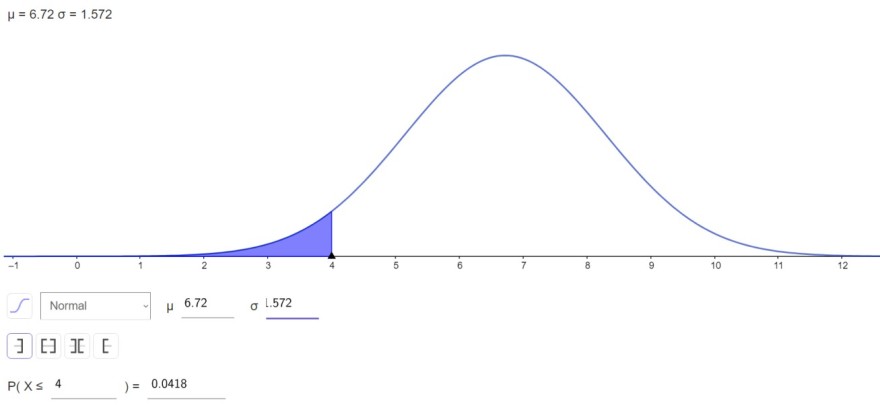
Die Wahrscheinlichkeit für weniger als 4, liegt hier bei 4%. Doch wenn man das von 1 abzieht kommt man annähernd auf die wirkliche Wahrscheinlichkeit.