Erwartungswert der Anzahl der notwendigen Drehungen & Varianz

Question

Hallo community,

ich komme bei diesem beispiel egal welchen weg ich durchdenke einfach micht weiter. hab morgen meine sa und bin schon etwas verzweifelt. danke im voraus.

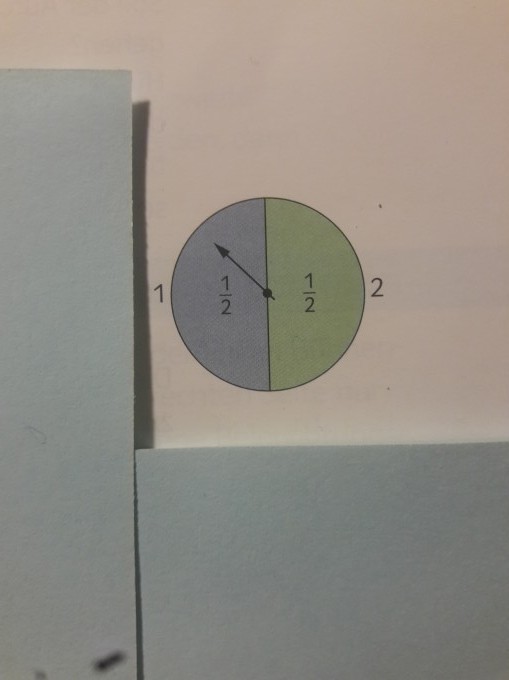
Aufgabe: bei dem nebenstehend abgebildeten glücksrad erhält man so viel ausbezahlt wie die zahl am rand des jeweiligen sektors angibt. das glücksrad wird so oft gedreht bis die summe der erhaltenen gewinne mindestens 4 ist. es sei N die anzahl der dazu notwendigen drehungen. Berechne E(N) und V(N) !

schönen abend noch

Answer 1

μ=1*1/2+2*1/2=1.5

σ=1^2*1/2+2^2*1/2-1.5^2=1/4

das glücksrad wird so oft gedreht bis die summe der erhaltenen gewinne mindestens 4 ist. es sei N die anzahl der dazu notwendigen drehungen.

1+1+1+1=4 also ganze vier Mal.

Answer 2

Das könnte so aussehen:

Comments

aber wieso hat man bei ni=3 5 möglichkeiten?? wären es nicht 3? denn die summe der zahlenkombi 2,2,1 ergibt doch 5 und nicht 4?

---

das glücksrad wird so oft gedreht bis die summe der erhaltenen gewinne mindestens 4 ist.

Erstmal habe ich 221 gar nicht erfasst, weil nach 22 schon aufgehört wird. zum anderen ist 5 doch mindestens 4 oder nicht?