Hallo,
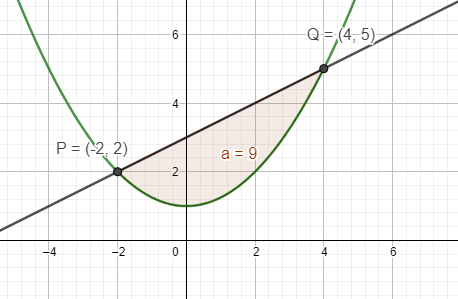
stelle die Gleichung der Geraden zwischen P und Q auf.
zum Vergleich:
[spoiler]
Steigung \(m=\frac{5-2}{4+2}=0,5\)
allgemeine Geradengleichung y = mx + n
Einsetzen der Koordinaten von P in die Gleichung ergibt \(2=0,5\cdot (-2)+n\Rightarrow n = 3\)
Somit lautet die Gleichung y = 0,5x + 3
zum Vergleich:
[/spoiler]
Bilde die Differenzfunktion zwischen der Geraden und der Parabel und berechne den Flächeninhalt zwischen P und Q.
[spoiler]
\(h(x)=0,25x^2+1-(0,5x+3)=0,25x^2-0,5x-2\\ H(x)=\frac{1}{12}x^3-0,25x^2-2x\\ H(-2)=\frac{7}{3}\\ H(4)=-\frac{20}{3}\\ A=\frac{7}{3}-\bigg(-\frac{20}{3}\bigg)=9\)
[/spoiler]
Gruß, Silvia
