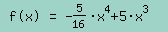d Für jeden Wert von u mit u e IR, 0 <u<14 sind die Punkte R(u l f (u)), Q(u l 0) und S(u-4 l 0) Eckpunkte eines Dreiecks.
Zeigen Sie, dass der Flächeninhalt des Dreiecks mit der Gleichung A(u)=-5/8*u^4+10u^3 berechnet werden kann.
e Genau ein Dreieck SQR aus Teilaufgabe d) besitzt einen maximalen Flächeninhalt. Ermitteln Sie diesen.
Für jede reelle Zahl a ist eine in IR definierte Funktion h mit h(x)=5ax² gegeben.
Text erkannt:
\( f(x)=-\frac{5}{16} \cdot x^{4}+5 \cdot x^{3} \)