Bestimmung einer rekursiven Formel

Question

Aufgabe:

Stell dir vor du hast ein unendlich großes Spielfeld. Dies ist folgendermaßen aufgebaut:
- Am Anfang gibt es ein Viereckiges Feld, genannt Feld 1
- Dieses teilt sich in 2 weitere Felder auf.
- diese Teilen sich wieder jeweils in 2 weitere auf
- usw..





Auf dieses Spielfeld können Bälle nach Folgenden Regeln gelegt werden:
- in jedes Feld darf nur ein Ball
- Damit in ein Feld ein Ball gelegt werden darf, muss das Feld vorher einen Ball enthalten
- also das Feld, welches sich in zwei teilte, um das Feld auf welches jetzt ein Ball gelegt werden soll zu erzeugen
- Beispiel:

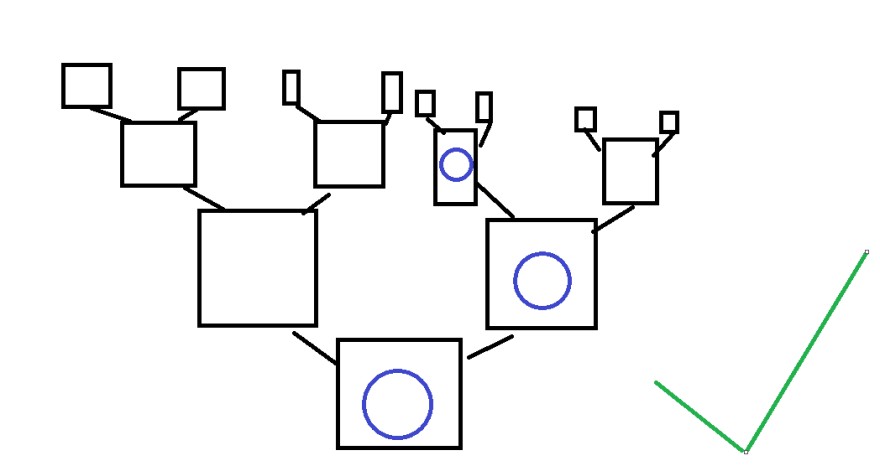
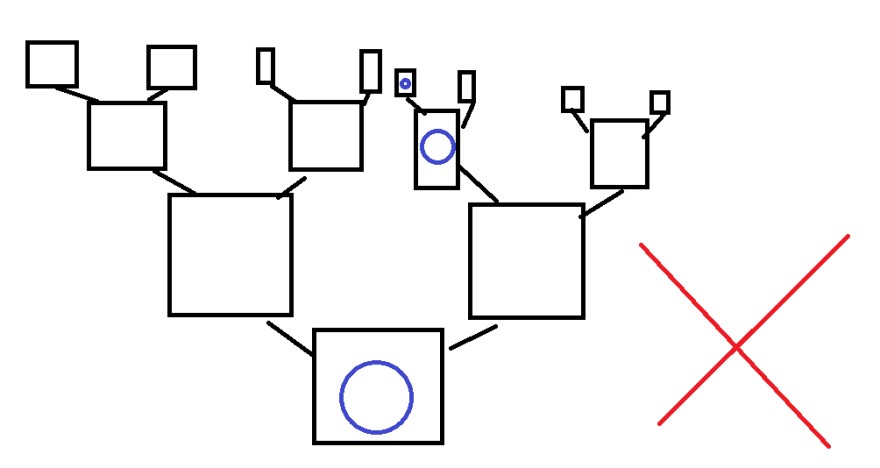
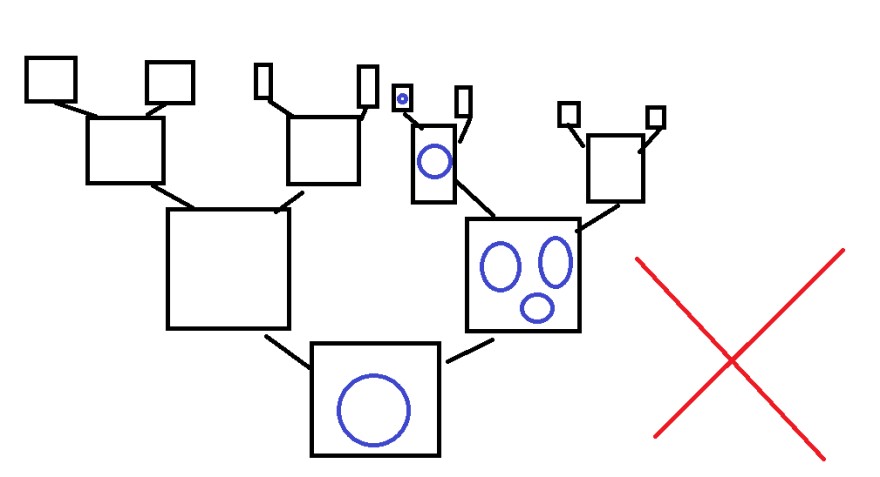
Nun gibt es noch eine andere Bezeichnung, Sackgassen. Ein Abschnitt ist eine Sackgasse, wenn nach einem Ball ein leeres Feld ist:



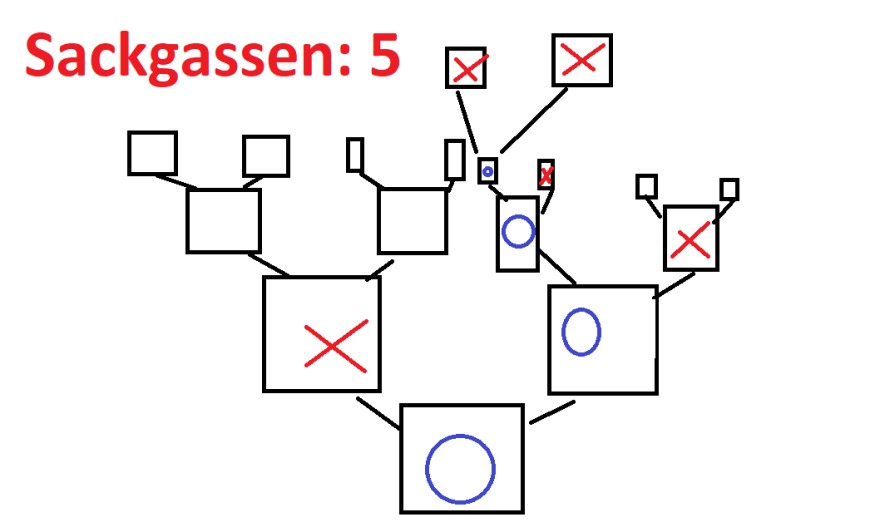
In jedem Spielfeld gibt es genau S_n Sackgassen. Du sollst ermitteln, wie viele Möglichkeiten es gibt genau S₄ und S₅ Sackgassen hervorzurufen. S₁ = 1, S₂ = 2, S₃ = 2

Dann sollst du ein Verfahren finden, um theoretisch zu ermitteln wie viele Möglichkeiten es gibt, für jede natürliche Zahl n so viele Sackgassen hervorzurufen. Diese Nummer wird in der variable S_n gespeichert. Du kannst dabei dich auf eine vorherige Anzahl von Sackgassen beziehen.

Problem/Ansatz:

Dann habe ich angefangen, S₄ und S₅ durch aufzeichnen herauszufinden. S₄ = 5 und S₅ = 12. Allerdings habe ich keine Ahnung wie man allgemein alle S_n ermitteln kann. Kann mir jemand dabei helfen? Vielen Dank im Voraus

Comments

Was genau ist denn \(n\)?

---

wie viele Möglichkeiten es gibt

Du solltest mitteilen, ob Ballkonfigurationen, die durch Spiegelung auch nur eines Teil-Baumes entstehen, als gleich oder als verschieden anzusehen sind.

Answer 1

Könntest du mal erläutern welche 2 Möglichkeiten es gibt 2 Sackgassen einzuzeichnen? Ich komme dort nur auf eine Möglichkeit.

Es gibt hier einen Zusammenhang zu den Catalan-Zahlen

https://de.wikipedia.org/wiki/Catalan-Zahl