Winkelfunktionen Parameter bestimmen

Question

Aufgabe:

Ich brauche hilfe bei den Parametervariationen von Winkelfunktionen

Problem/Ansatz:

Text erkannt:

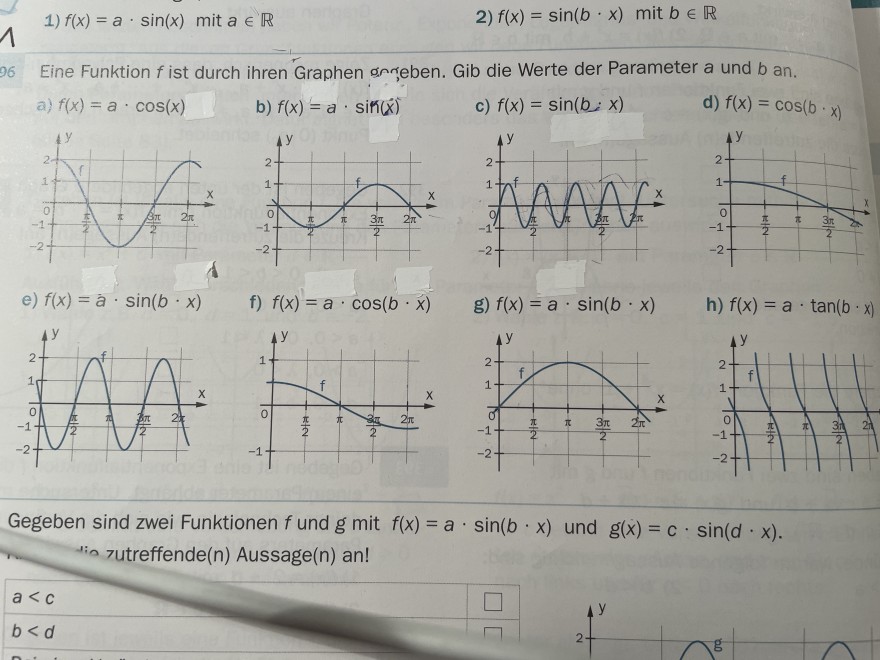
1) \( f(x)=a \cdot \sin (x) \) mit \( a \in \mathbb{R} \)
2) \( f(x)=\sin (b \cdot x) \) mit \( b \in \mathbb{R} \)
Eine Funktion \( f \) ist durch ihren Graphen onreben. Gib die Werte der Parameter a und \( b \) an.
a) \( f(x)=a \cdot \cos (x) \)
b) \( f(x)=a \cdot \sin (x) \)
c) \( f(x)=\sin (b ; x) \)
d) \( f(x)=\cos (b \cdot x) \)
e) \( f(x)=a \cdot \sin (b \cdot x) \)
f) \( f(x)=a \cdot \cos (b \cdot x) \)
g) \( f(x)=a \cdot \sin (b \cdot x) \)
h) \( f(x)=a \cdot \tan (b \cdot x) \)
Gegeben sind zwei Funktionen \( f \) und \( g \) mit \( f(x)=a \cdot \sin (b \cdot x) \) und \( g(x)=c \cdot \sin (d \cdot x) \). iio zutreffende(n) Aussage(n) an!
\( \begin{array}{l} a<c \\ b<d \end{array} \)

Answer 1

a)   cos(0)=1 , weil hier f(0)=2 ist, ist a=2

b)  versuche analog zu a) mit f(pi/2) !