Eine Alternative zu Teamwork

Question

Teamwork

Es gibt heute kaum noch einen Pädagogen, der Teamarbeit (an Stelle von Einzelarbeit) nicht für äußerst wichtig hält. Meistens werden dann nach der Aufgabenstellung Gruppentische gebildet und eine Aufgabe an alle Gruppen oder jeder Gruppe eine Gruppenaufgabe gestellt. Die verschiedenen Gruppen kommunizierten im Allgemeinen nicht miteinander. In der Umsetzung dieses sehr starren Vorgehens lassen sich auch Nachteile der Teamarbeit identifizieren:

	Das Durchdringen einer Fragestellung kann nur in einer Phase individueller Konzentration gelingen. Aus der Gruppe können Ablenkungen kommen, die eine tiefere Durchdringung der Aufgabenstellung behindert.
	Abhängigkeit der Qualität der Arbeit, von der Leistungsfähigkeit auch schwächerer Teammitglieder. Bei jeder             Mannschaftsleistung beeinflussen individuelle Fehlleistungen das Gesamtbild (z.B im Mannschaftssport).
	Gruppendynamische Prozesse wirken auf das Gruppenergebnis, wenn sich Meinungen von Gruppenmitgliedern        durchsetzen, die über Persönlichkeit verfügen, ohne die Arbeit voranzubringen. Selbstdarstellung dominiert          gegenüber Fachkompetenz.
	Gruppenangehörige können fehlende Fähigkeiten und Motivationen hinter Leistung und Motivation engagierter           Mitglieder verbergen.

Diese Nachteile werden in folgender flexibler Organisationsform minimiert:
Jeder beginnt zunächst einmal in stiller Einzelarbeit ohne Gruppeneinteilung mit dem Ziel, die Aufgabe zu lösen. Dabei entwickelt jeder seinen persönlichen Blick auf die gestellte Aufgabe. Das hat einerseits den Vorteil, dass sehr viele Facetten der Aufgabe erkannt werden und andererseits, dass sich wirklich jeder mit der gestellten Aufgabe auseinandersetzt. Sobald jemand etwas nicht versteht oder Klärungsbedarf hat, wendet er sich an eine/n Kolleg*in, von der/m sie /er annimmt, dass diese/r ihm Klarheit verschaffen kann. Dabei können auch temporär Kleingruppen entstehen, die sich im Falle einer Klärung wieder auflösen. Dann kehrt jeder in die Einzelarbeit zurück. Dieser Wechsel zwischen Einzelarbeit und Arbeit in Kleingruppen wiederholt sich nach Bedarf, wobei sich die Kleingruppen auch immer wieder neuformieren können. Wenn eine Mehrheit des Plenums glaubt, zu einem Ergebnis gekommen zu sein, werden von Freiwilligen unterschiedliche Lösungen vorgetragen und im Plenum diskutiert. Wenn es erforderlich ist, dass eine Lösung unter mehreren ausgewählt werden muss, sollte dies ganz am Schluss durch Mehrheitsbeschluss des Plenums geschehen. In jedem Falle aber sollte die Einheit mit der Formulierung eines überwiegend akzeptierten Ergebnisses enden.

Beispiel für einen Unterrichtsentwurf zu dem flexiblen Vorgehen:

Entdeckung des Satzes von Pythagoras
Jede/r Schüler*in erhält ein Din-A-4-Blatt mit dem Aufdruck eines sogenannten ‚Römischen Verbundes‘ (siehe Abbildung). Der römische Verbund ist eine Paketierung der Ebene mit quadratischen Fliesen A und B zweier verschiedener Größen:

Darunter steht folgender Aufgabentext: Die Seitenlängen der Fliesen A und B seien a und b. Zeichne auf den römischen Verbund ein rechtwinkliges Dreieck mit den Kathetenlängen a und b, sodass die Katheten parallel zu den Fliesenfugen oder ganz auf Fliesenfugen liegen. Die Hypotenuse (Bezeichnung und Länge) dieses Dreiecks sei c. Zeichne ein Gitter von Quadraten C mit der Seitenlänge c auf das römische Parkett. Dabei soll die Strecke c ihre zuerst gewählte Lage beibehalten. Welche Beziehung besteht zwischen den Flächen von A, B und C?
Es ist davon auszugehen, dass es Nachfragen zur Aufgabenstellung gibt. Diese können in einer vorgeschalteten Frontalunterrichtsphase vom Lehrer beantwortet werden. Der Stundenverlauf wurde oben bereits geschildert.

Da von den rechtwinkligen Dreiecken nur gefordert ist, dass ihre Katheten parallel zu den Parkettfugen verlaufen oder mit Abschnitten davon identisch sind, sind viele verschiedene Eintragungen in das vorgelegte Blatt denkbar. Die Lösungsidee, das Quadrat C entlang der Parkettfugen zu zerschneiden, werden nicht alle Schüler*innen finden, obwohl die Schnittlinien bereits gezeichnet wurden. Zu Vorträgen im Plenum werden sich vermutlich nur solche Schüler*innen melden, welche die Lösungsidee gefunden haben. Am Schluss sollte erkannt werden, dass alle richtigen Lösungen gleichwertig sind und eine Abstimmung höchstens bezüglich der zweckmäßigsten Lage des Quadrates C auf dem Römischen Verbund erfolgen kann. Abschließend sollte eine Formulierung des Aufgabenergebnisses gefunden werden, die möglichst großen Konsens findet.

Eine von vielen möglichen Lösungen ist die nachstehende. Die Farben rot, grün, blau und gelb bedecken einerseits die Quadrate A und B und andererseits auch das Quadrat C:

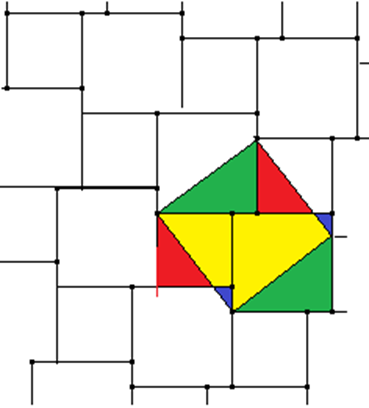
Damit gilt: Fläche_(A)+Fläche_(B)=Fläche_(C)
oder:
Im rechtwinkligen Dreieck mit den Kathetenlängen a und b sowie der Hypotenusenlänge c gilt a^²+b^²=c^².

Auch andere Schüler*innen, die das Dreieck an eine andere Stelle des Römischen Verbundes gelegt haben, können die Flächengleichheit in eben dieser Weise zeigen. Nun können verschiedene Lösungen an einem Softboard nebeneinandergestellt werden. Als Hausaufgabe bietet sich an, das Stundenergebnis in einem römischen Verbund mit selbstgewählten Seitenlängen der Einzelquadrate zu demonstrieren.