Im ersten Stück vom Ursprung nach rechts bleibt der Winkel bei 0° (bzw im Bogenmaß bei 0), während der Betrag des wandernden Punktes von 0 auf 1 wächst. Für dieses Wachsen stehen dir Parameterwerte von 0 bis 0,25 zur Verfügung.
Damit ist die Parametrisierung hier einfach z(t)=4t mit 0≤t<0,25.
Im anschließenden Bogen bleibt r konstant 1, während der Winkel von 0 auf π wächst. Wenn dein Parameter t auch hier bei 0 beginnen dürfte (und bis 0,5 gehen würde), wäre das mit z(t)=exp(2tπ·i) machbar. Da dein t zum Start des Bogens aber schon 0,25 ist, müssen wir korrigieren zu
z(t)=exp(2(t-0,25)π·i) mit 0,25≤t<0,75.
Nur könntest du die Hälfte der noch verbleibenden Parameterspanne (der Bereich von t=3/4 bis t=1 ist noch frei) nutzen, um mit t=3/4 bis t=7/8 vom Punkt (-1, 0) zum Punkt (-0,6 ; 0) zu gehen.
z(t)= - 1+3,2(t-3/4) mit 3/4≤t<7/8.
(Überzeuge dich davon, dass du mit t=3/4 im Punkt (-1 , 0) und mit t=7/8 im Punkt (-0,6 , 0) bist.
Der letzte Halbkreis ist etwas verzwickt...
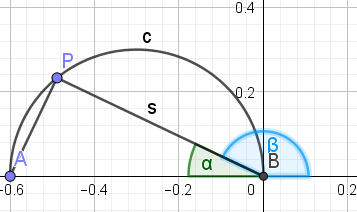
Der Punkt P muss noch von A nach B wandern. Dazu ist es notwendig, dass der eingezeichnete Winkel α von 0 bis 90° (also bis π/2) wächst. Da wir t schon bis 7/8 verbraucht haben, muss man mit t=7/8 den Winkel 0 und mit t=1 den Winkel π/2 bekommen. Das erreichen wir mit α= 4π(t-7/8).
Allerdings wird die Lage des Punktes P in der GZE nicht durch alpha, sondern durch den eingezeichneten Winkel beta charakterisiert. Es gilt β=π- 4π(t-7/8).
Jetzt brauchen wir noch den in der Zeichnung mit s bezeichneten Abstand von P zum Ursprung. Nach dem Satz des Thales ist das Dreieck ABP rechtwinklig, und es gilt s=0,6*cos α bzw. s=0,6*cos(4π(t-7/8)).
Die fett hervorgehobenen Terme kannst du noch vereinfachen und in die Exponentialform einsetzen.