Hallo,
Willkommen in der Mathelounge!
mache Dir das am besten an der bildliche Darstellung klar. Ich habe hier zwei Versuche unternommen, das zu erklären, Einmal in 3D und einmal in 2D (s.u.)
Das zweifache Kreuzprodukt im Anschauungsraum (3D) sieht so aus:
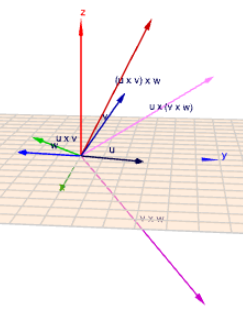
Klicke auf das Bild und rotiere die Szene mit der Maus, so dass Du einen guten räumlichen Eindruck erhältst. Und denke Dir dann jedes Vektorprodukt als den Vektor, der auf den beiden Argumentvektoren senkrecht steht. Dann sollte klar werden, dass im Allgemeinen diese beiden Produkte nicht gleich sind.$$(u \times v) \times w \ne u \times (v \times w)$$
Ich habe den Vektor \(w\) geändert auf \(w=(4|\,-2|\,1)\), damit die Vektoren nicht zu dicht zusammen liegen. Auch habe ich im Bild die Längen der Kreuzprodukte gekürzt. Auf die Längen der Vektoren kommt es aber gar nicht an!
Alternativer Ansatz mit homogenen Koordinaten
Solltest Du dich mit der räumlichen Vorstellung schwer tun, hier ein Versuch, das ganze in einer Ebene (2D) abzubilden.
Ich betrachte nur Vektoren deren dritte Koordinate \(z=x_3=1\) ist. Weiter ist auch nur die Ebene \(x_3=1\) interessant, und die bilde ich hier ab. Das Kreuzprodukt zweier Vektoren \(u\) und \(v\) aus dieser Ebene berechnet sich zu $$\begin{pmatrix} u_x\\u_y \\ 1 \end{pmatrix} \times \begin{pmatrix} v_x\\v_y\\ 1 \end{pmatrix} = \begin{pmatrix} u_y-v_y\\v_x-u_x\\ u_xv_y - u_yv_x \end{pmatrix} = f\begin{pmatrix} \frac{u_y-v_y}{f} \\ \frac{v_x-u_x}{f} \\ 1 \end{pmatrix} \quad\quad f = u_xv_y - u_yv_x$$Im folgenden betrachte ich nur das mit den Faktor \(f\) multiplizierte Kreuzprodukt. Ich schrieb oben bereits, dass die Länge für unsere Untersuchungen keine Rolle spielt.
Oben habe ich das dargestellt. \(u\) und \(v\) sind zwei Punkte (sozusagen die Spitzen der Vektoren) in der Ebene \(x_3=1\). Das Ergebnis des Kreuzprodukts \(u \times v\) ist als Strecke mit Beginn im Ursprung dargestellt. Die gestrichelte Gerade durch \(u\) und \(v\) ist die Schnittgerade der Ursprungsebene, die durch \(u\times v\) definiert ist, mit der Ebene \(x_3=1\).
Und dieses Paar "Vektor bzw. Punkt in \(x_3=1\)" und "Gerade" ist eindeutig. Man kann jedem Punkt in \(x_3=1\) eine Gerade zuordnen und umgekehrt. Und das Kreuzprodukt zweier beliebiger nicht identischer Vektoren auf eben dieser Geraden ergibt wieder den selben Punkt.
Das nennt man Dualität von Punkt und Gerade.
Und nun das ganze mit drei Vektoren \(u\), \(v\) und \(w\):
Das Kreuzprodukt \(u \times v\) habe ich hier nur als (roten) Punkt dargestellt. Und das Kreuzprodukt \((u\times v) \times w\) ist dann stellvertretend die rote gestrichelte Gerade, die natürlich durch \(w\) verläuft (s.o.), bzw. analog dazu das Ende der roten Strecke, die vom Ursprung ausgeht.
Genau das gleiche habe ich für \(u \times (v \times w)\) gemacht, diesmal das ganze in grün. Beide Produkte wären genau nur dann identisch (zumindest was ihre Richtung betrifft), wenn die gestrichelten Geraden identisch wären. Das ist im Allgemeinen aber nicht der Fall!
Schiebe aber mal den Punkt \(w\) nach \((1|-2)\) und \(v\) nach \((-1|0))\).
Gruß Werner