Hallo,
die Form einer Geradengleichung lässt sich ausdrücken durch y = mx + b
m ist die Steigung, n der Schnittpunkt mit der y-Achse.
a) Zeichne n ein:
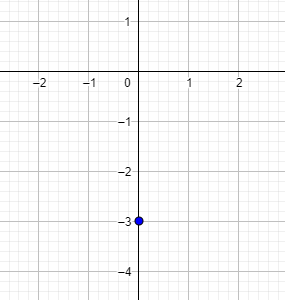
Gehe immer eine Einheit nach rechts, und dann entsprechend viele Einheiten nach oben bei positiver Steigung, oder entsprechend viele Einheiten nach unten bei negativer Steigung, um den zweiten Punkt einzuzeichnen. Anschließend verbindest du die beiden Punkte.
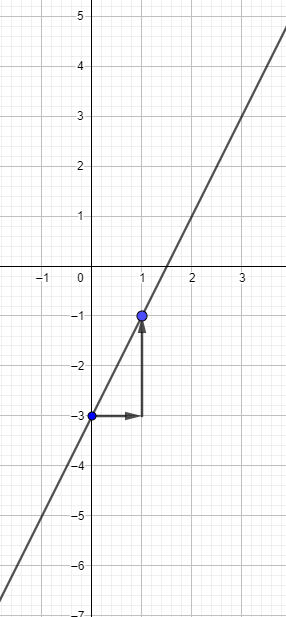
Melde dich, wenn du noch Fragen hast.
Gruß, Silvia