Aufgabe:
Es ist der getönte Flächeninhalt über der Kurve zu berechnen. Gegeben ist die Skizze und die Funktion.
Problem/Ansatz:
Die richtige Lösung lt. LöBuch lautet: 3*ln (2+2) minus ∫ von -1 bis 2 ln(x+2) dx
Bei meiner Hilfe für meine Enkelin erschließt sich mir nicht der Ausdruck 3*ln(2+2) für das Rechteck.
Wäre euch für die Hilfe sehr dankbar.
Wolfgang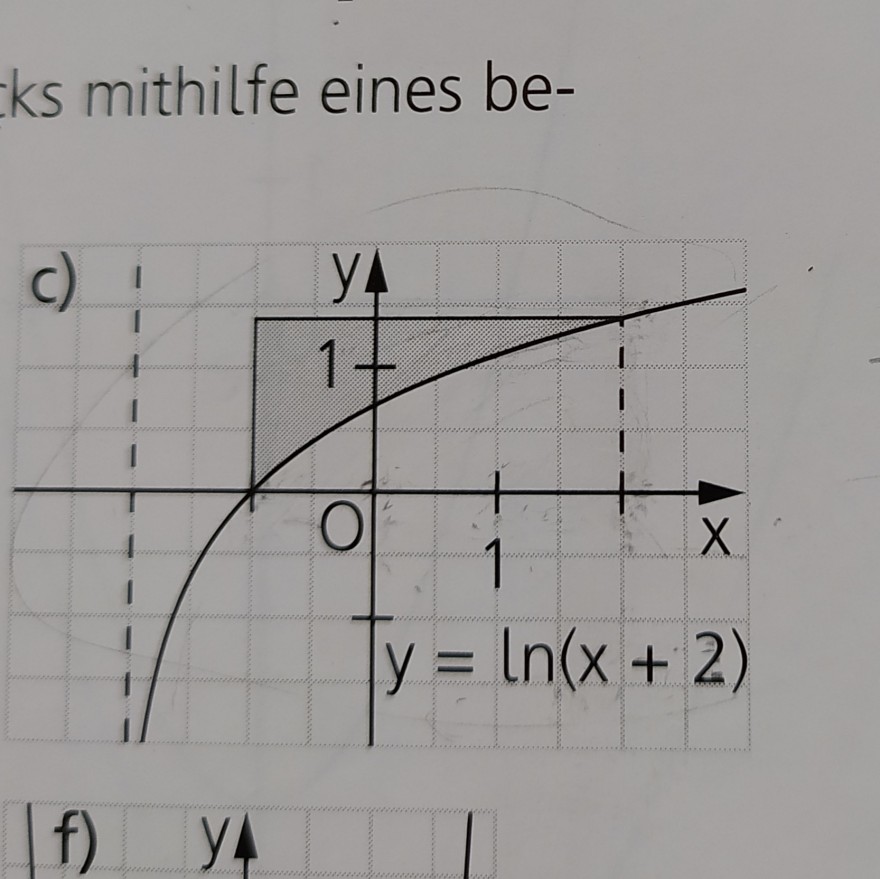
Text erkannt:
iks mithilfe eines be-
f) \( y \)