Bestimmung der Vorzeichen von fx' und fy' in zwei Punkten

Question

Die Aufgabe lautet: Die Abbildung zeigt einige Höhenlinien für eine Funktion z=f(x,y) zusammen mit der Geraden 2x + 3y = 12

a) Welche Vorzeichen haben fx' und fy' in den Punkten P und Q?

b) Bestimmen Sie mögliche Lösungen der Gleichung (i) f(1,y) =2 und (ii) f(x,2) = 2

c) Welches ist der grösste Wert von f(x,y) unter denjenigen (x,y), die 2x + 3y=12 erfüllen?

Irgendwie verstehe ich weder die Abbildung noch die Aufgabe. Was bedeutet die Gerade in der Ebene, und soll man die ableiten?

Answer 1

(a) Welche Vorzeichen haben fx' und fy' in den Punkten P und Q?

Stell dir vor, du hast eine Karte mit Höhenkurven vor dir. In x-Richtung hast du Osten und gegen oben Norden.

Wenn du nun in P stehst und Richtung Osten rennst, geht's steil bergauf. Daher ist f_x' in P positiv.

Wenn du gegen Norden rennst, geht's ganz leicht runter. Daher ist f_y' in P negativ.

In Q geht's gegen Osten runter und gegen Norden steil hoch.

Also f_x ' neg. und f_y' pos.

(ohne Gewähr)

( c) Welches ist der grösste Wert von f(x,y) unter denjenigen (x,y), die 2x + 3y=12 erfüllen?

Wenn du auf der Geraden rennst von links oben nach rechts unten auf der Karte, bist du ungefähr im Punkt (1,3) auf der Höhe z=1 rennst dann über die Höhenlinie z=2 und bist ungefähr im Punkt (2.5 | 2.5) auf der Höhe z=3. Ab jetzt geht's wieder runter. 

Der grösste z-Wert auf diesem Weg ist z=3.

(b) Bestimmen Sie mögliche Lösungen der Gleichung (i) f(1,y) =2 und (ii) f(x,2) = 2

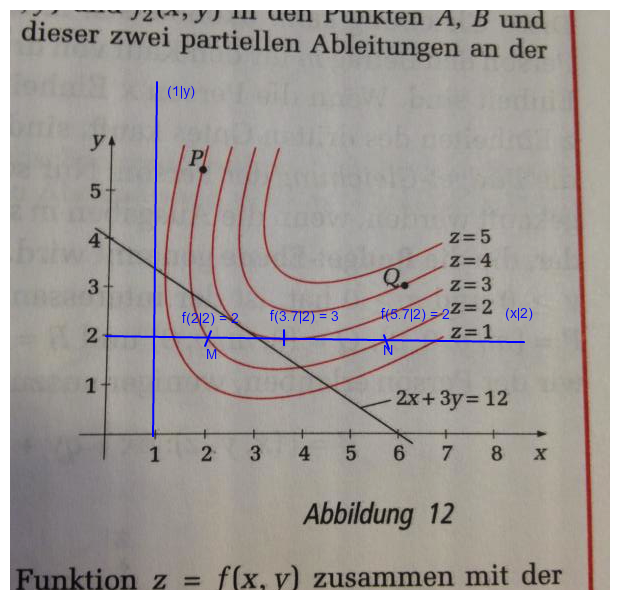
 (i) f(1,y) =2 Da die blaue Linie gegen Norden die Höhenkurve z=2 nicht schneidet, gibt es keinen entsprechenden Punkt. Es sei denn, du fügst noch weitere Höhenkurven hinzu, z.B. im Gebiet unterhalb der x-Achse.

(ii) f(x,2) = 2 hier sind die Punkte M und N möglich, die auf der blauen Geraden Richtung Osten liegen.

Comments

Vielen Dank, es war sehr hilfreich!! :D