Aufgabe: Ich soll folgende Reihen auf Konvergenz und absolute Konvergenz überprüfen.
…
Problem/Ansatz:
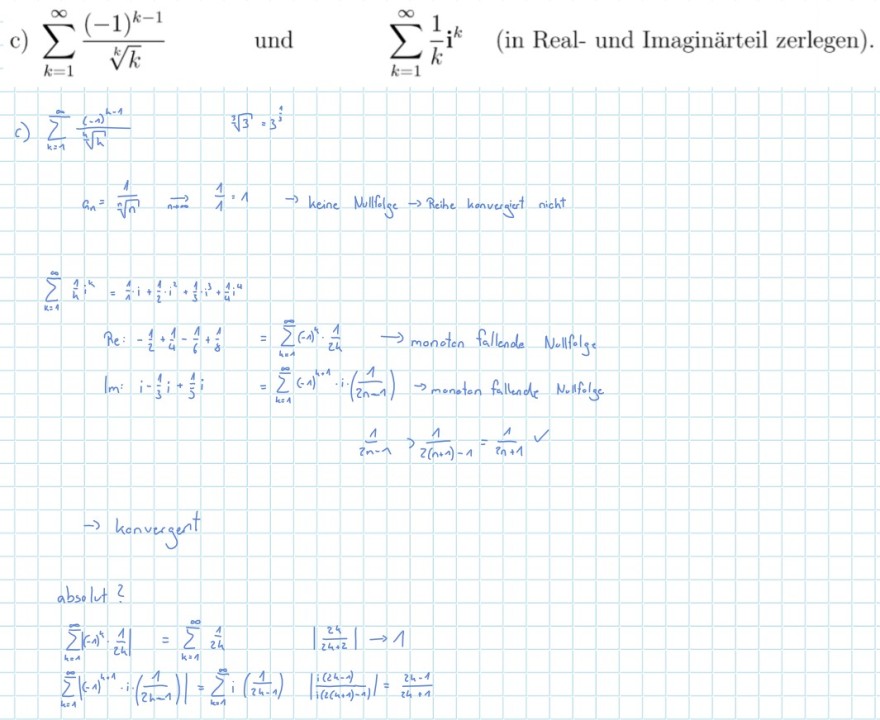
Text erkannt:
c) \( \sum \limits_{k=1}^{\infty} \frac{(-1)^{k-1}}{\sqrt[k]{k}} \quad \) und \( \quad \sum \limits_{k=1}^{\infty} \frac{1}{k} \mathbf{i}^{k} \quad \) (in Real- und Imaginärteil zerlegen).
c) \( \sum \limits_{k=1}^{\infty} \frac{(-2)^{h-1}}{\sqrt[3]{h}} \quad \sqrt[2]{3} \cdot 3^{3} \)
\( a_{n}=\frac{1}{\sqrt[3]{n}} \Rightarrow \frac{1}{1} \cdot 1 \rightarrow \) keine Milloge \( \rightarrow \) Reche Kanvergict nicht
\( \sum \limits_{k=1}^{\infty} \frac{1}{h} i^{k}=\frac{1}{i} i+\frac{1}{i} i^{2}+\frac{1}{3} j^{3}+\frac{1}{i^{4}} \)
Re: \( -\frac{1}{2}+\frac{1}{4}-\frac{1}{6}+\frac{1}{j}=\sum \limits_{i=1}^{n}(-1)^{4} \cdot \frac{1}{24} \rightarrow \) monoten fallende Nollfolge
Im: \( i-\frac{1}{3} i+\frac{1}{5} i=\sum \limits_{k=1}^{\infty}(-1)^{i)^{-1}} \cdot i \cdot\left(\frac{1}{2 n-1}\right) \rightarrow \) monoton fallende Norlifelge
\( \frac{1}{i n-1} \frac{1}{2(n+1)-1}=\frac{1}{2 n+1} \mathcal{} \)
\( \rightarrow \) konvergent
absolut?
\( \sum \limits_{k=1}^{n}\left|-(-1)^{k} \cdot \frac{1}{24}\right|=\sum \limits_{k=1}^{\infty} \frac{1}{24} \quad\left|\frac{24}{24 \cdot 2}\right| \rightarrow 1 \)
Kann ich das so begründen?
Also beim zweiten, dass das nicht absolut konvergiert?
Vielen Dank schonmal im Voraus