Lineare Funktion im Bereich Geometrie Dreiecke

Question

Aufgabe

Gegeben sind die Dreiecke ABCn. Dabei bewegen sich Punkte Cn auf der Geraden g mit
y = 1/2x + 3,5. Es gilt: A (-4| -1); B (2|1); Cn (× l 1/2x + 3,5)
Zeichne die Gerade g und die Dreiecke AB1 für x = -3 und ABC2 für x = 1 in ein Koordinatensystem.
Zeige durch Rechnung, dass das Dreieck ABC2 rechtwinklig ist.

Answer 1

Die Gerade x=1  schneidet y=1/2x+3,5  in C₂(1|4)

Der Mittelpunkt der Strecke AC₂ ist M(-1,5|1,5). Bestimme nun die Länge der Strecke MA. Das ist der Radius des Thaleskreis über A C₂.

Jetzt musst du nur noch den Nachweis führen, dass B auf diesem Kreis liegt.

Answer 2

Hallo,

zeichnen ist nicht so schwierig.

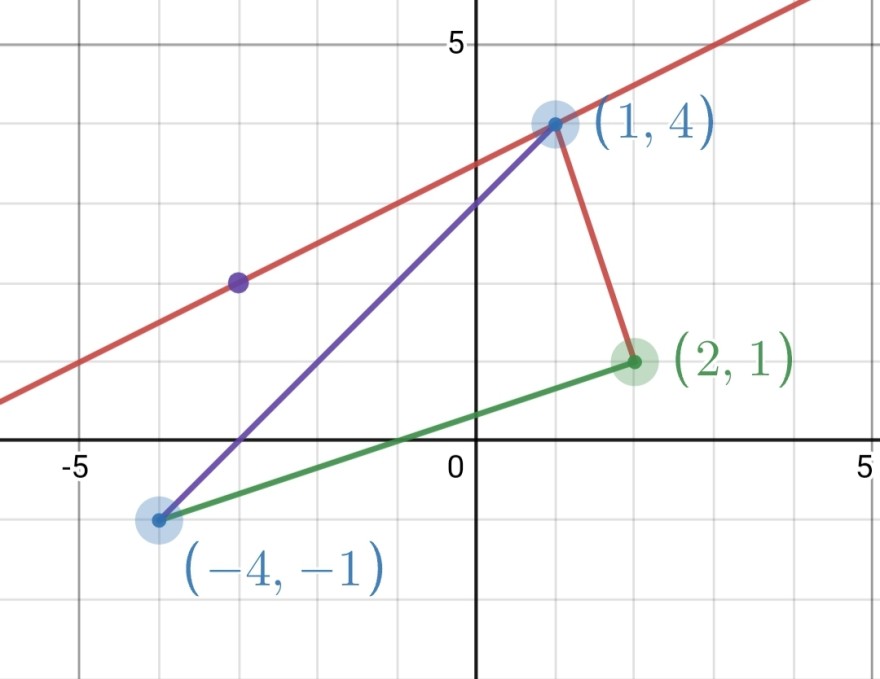
Der rechte Winkel liegt offensichtlich bei B.

Nun berechne ich die Steigungen der Geraden durch A und B, sowie der Geraden durch B und C2.

A (-4| -1); B (2|1);

Cn (× l 1/2x + 3,5) → C2(1|4)

m1 = m(AB) = (1-(-1)) / (2-(-4)) = 2/6 = 1/3

m2 = m(BC2) = (4-1)/(1-2) = -3

m1 • m2 = ⅓•(-3) = -1

--> Beide Geraden verlaufen orthogonal.