Aufgabe:
Text erkannt:
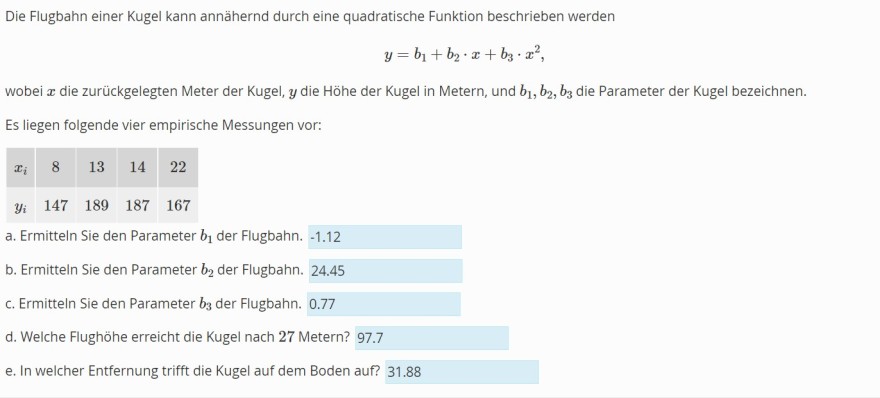
Die Flugbahn einer Kugel kann annähernd durch eine quadratische Funktion beschrieben werden
\( y=b_{1}+b_{2} \cdot x+b_{3} \cdot x^{2}, \)
wobei \( x \) die zurückgelegten Meter der Kugel, \( y \) die Höhe der Kugel in Metern, und \( b_{1}, b_{2}, b_{3} \) die Parameter der Kugel bezeichnen.
Es liegen folgende vier empirische Messungen vor:
\begin{tabular}{|c|c|c|c|c|}
\hline\( x_{i} \) & 8 & 13 & 14 & 22 \\
\hline\( y_{i} \) & 147 & 189 & 187 & 167 \\
\hline
\end{tabular}
a. Ermitteln Sie den Parameter \( b_{1} \) der Flugbahn. \( -1.12 \)
b. Ermitteln Sie den Parameter \( b_{2} \) der Flugbahn. \( 24.45 \)
c. Ermitteln Sie den Parameter \( b_{3} \) der Flugbahn. \( 0.77 \)
d. Welche Flughöhe erreicht die Kugel nach 27 Metern? \( 97.7 \)
e. In welcher Entfernung trifft die Kugel auf dem Boden auf? \( 31.88 \)
Problem/Ansatz:…da ich alles mit online rechner ausgerechnet habe, aber irgendwo habe ich fehler gemacht. Checkt jemand wo der Fehler liegt?
so habe ich gerechnet:
147=b1+b2*8+b3*64
189=b1+b2*13+b3*169
187=b1+b2*14+b3*196
167=b1+b2*22+b3*484
da habe ich dann A*B (online rechner ) folgende ergebnisse bekommen:
b1= 690
b2=9920
b3=158829
danach habe ich folgendes in matritx rechner eingegeben
4 57 913 690
57 913 16101 9929
913 16101 305329 158829
hier habe ich folgende ergebnisse:
-12
24,45
-0,77
das habe ich eingesetzt, sieh oben.
Aufgabe d) habe ich so berechnet :
y= -1,12+24,45*x+(-0,77)*x^2
da habe ich x=27 eingesetzt und als lösung 97, 7 bekommen.
Aufgabe e)
0= -0,7657904344651333*x^2+24,45029067318224*x+(-1,1249754261802423)
ergebniss: 31,88
könnte jemand kontrolieren und vielleich helfen. ich bedanke mich herzlich