§1: Natürlich hat das was mit Grenzwerten zu tun! Nur weil eine Teil-Funktion in einem Punkt gegen -∞ strebt (das ist etwas anderes als UNDEFINIERT!), deshalb muss der Grenzwert der kompletten Funktion nicht auch undefiniert sein. Durch Umstellung kommt man zur eigentlichen Funktion:
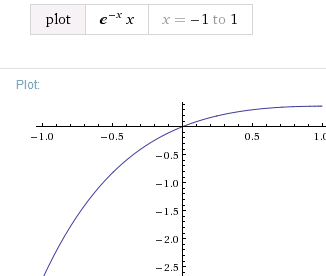
exp(log(x)-x) = x * e^{-x}
§2 Die Reihenentwicklung der kompletten Funktion um x=0 ist auch eindeutig definiert! Ganz eindeutiger Durchgang durch den Nullpunkt!
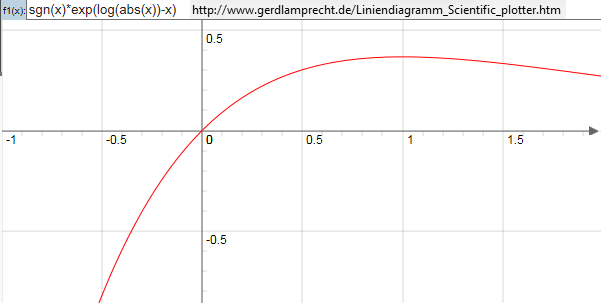
§3 Die Grafiken sind auch eindeutig ohne Sprünge und in jedem Punkt ableitbar:
d/dx exp(log(x)-x) = e^{-x} * (1-x)
zurück per Integration: integrate e^{-x}*(1-x) dx = x * e^{-x} wieder die eigentliche überall definierte Funktion!
§4: Es gibt sogar viele Funktionen, die Teilfunktionen mit 1/x beinhalten und als ganze Funktion genau wie diese hier durchgängig zeichenbar und ableitbar sind.
So könnte ich fast in jede Funktion, die durch den Ursprung verläuft durch Umstellung was mit log(x) einbauen -> und dann würden diese alle plötzlich in diesem Punkt nicht mehr definiert sein -> das wäre schlimm!
Ich habe schon viele Funktionen für den kompletten reellen Zahlenbereich (manchmal auch komplexe Z.) gültig gemacht, wo alte Professoren mit ihren alten Sprüchen "...ist aber nur für ganze Zahlen definiert" festhielten. (Fakultät, Fibonacci(x), StirlingS1(x,2) per hypergeometrische Funktionen)