Aufgabe:
Ein Designer verkauft sein T-Shirt momentan ohne jegliches Logo. Er vermutet, das T-Shirt könnte die Kunden besser ansprechen, wenn er es mit dem Logo eines Reiters verkauft. Deshalb führt er folgende Kundenbefragung durch: Es werden 12 Testpersonen ausgewählt. Zunächst lässt man sie das T-Shirt ohne Logo bewerten und fragt nach einer Bewertung auf einer Skala von 1 (schlecht) bis 10 (gut). Dann lässt man sie das T-Shirt mit dem Logo anprobieren und fragt nach einer weiteren Bewertung.
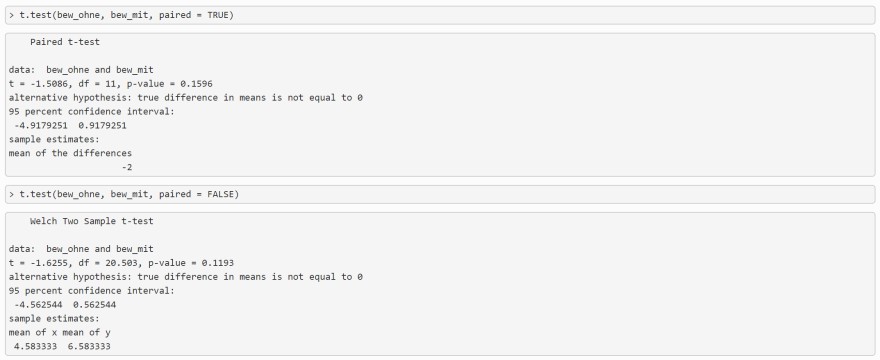
Wie groß ist der p-Wert, wenn die Alternativhypothese lautet, dass die Bewertung mit Logo im Schnitt schlechter ausfällt? Die folgenden R-Outputs stehen Ihnen dabei zur Verfügung:
Text erkannt:
> t.test(bew_ohne, bew_mit, paired = TRUE)
Paired t-test
data: bew_ohne and bew_mit
\( t=-1.5086 \), df = 11 , p-value \( =0.1596 \)
alternative hypothesis: true difference in means is not equal to o
95 percent confidence interval:
\( -4.9179251 \) Q.9179251
sample estimates:
mean of the differences
\( >t \).test(bew_ohne, bew_mit, paired = FALSE)
Welch Two Sample t-test
data: bew_ohne and bew_mit
\( t=-1.6255 \), df \( =20.503 \), p-value = \( 0.1193 \)
alternative hypothesis: true difference in means is not equal to o
95 percent confidence interval:
\( -4.562544 \) o. 562544
sample estimates:
mean of \( x \) mean of y
\( 4.583333 \) 6.583333
Problem/Ansatz:
Ich weiß nicht, wie ich vorgehen soll. Kann mir jemand helfen?