Aufgabe:
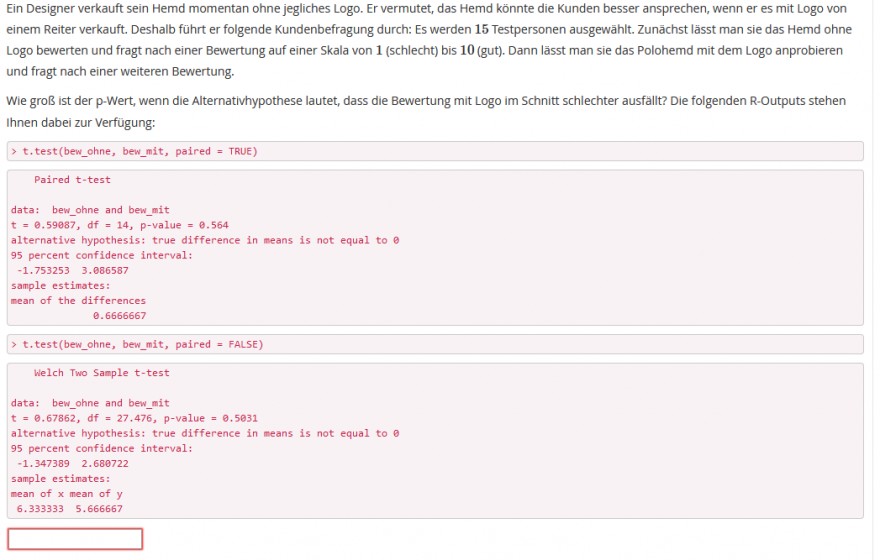
Text erkannt:
Ein Designer verkauft sein Hemd momentan ohne jegliches Logo. Er vermutet, das Hemd könnte die Kunden besser ansprechen, wenn er es mit Logo von einem Reiter verkauft. Deshalb führt er folgende Kundenbefragung durch: Es werden 15 Testpersonen ausgewàhlt. Zunāichst lässt man sie das Hemd ohne
Logo bewerten und fragt nach einer Bewertung auf einer Skala von 1 (schlecht) bis 10 (gut). Dann lässt man sie das Polohemd mit dem Logo anprobieren
und fragt nach einer weiteren Bewertung.
Wie groß ist der p-Wert, wenn die Alternativhypothese lautet, dass die Bewertung mit Logo im Schnitt schlechter ausfallt? Die folgenden R-Outputs stehen
Ihnen dabei zur Verfugung:
> t.test(bew_ohne, bew_mit, paired - TRUE)
Paired t-test
data: bew ohne and bew_mit \( t=0.59087, d f=14, p \) -value \( =0.564 \)
alternative hypothesis: true difference in means is not equal to \( \theta \) 95 percent confidence interval:
\( \begin{array}{ll}-1.753253 & 3.086587\end{array} \)
sample estimates:
mean of the differences
0.6666667
t.test(bew_ohne, bew FALSE)
Welch Two sample t-test
data: bew_ohne and bew mit \( t=0.67862, d f=27.476, p \) -value \( =0.5031 \)
alternative hypothesis: true difference in means is not equal to \( \theta \) 95 percent confidence interval:
\( \begin{array}{ll}-1.347389 & 2.680722\end{array} \)
sample estimates:
mean of \( x \) mean of \( y \) \( 6.333333 \quad 5.666667 \)
Problem/Ansatz:
kann mir bitte jemad helfen