Fünfeck Parallelität zweier Seiten beweisen

Question

Aufgabe:

Wie beweise ich, dass in einem regelmäßigen Fünfeck die Strecke AB parallel zur Strecke EC ist.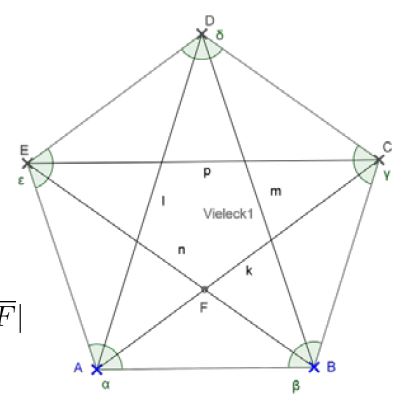

Problem/Ansatz:

Ihr seht oben das Bild eines regelmäßigen Fünfecks. Wir sollen beweisen, dass |AB| || |EC|

Ich habe mir überlegt, dass man das Dreieck EFC konstruieren kann, woraus die Parallelität folgt.

1. Dreieck ABF wird um den Punkt F gedreht, F = Fixpunkt

2. es erfolgt eine Streckung bis B=C und A=E

3. eine Strecke, die um 180 gedreht/gespiegelt wurde, ist immer parallel zur Originalstrecke

Das war meine Überlegung, aber bin mir unsicher, ob man das so schreiben kann/darf.

Vielleicht hat jemand von euch eine bessere Lösung :)

Dankeee

Answer 1

Hallo

ich würde aus der Gleichheit der Strecken von F aus die Umkehrung des Strahlensatzes benutzen. Aber deine Argumente sind sich ok

Gruß lul

Answer 2

Hallo,

2. es erfolgt eine Streckung bis B=C und A=E

Dies ist nur genau dann möglich, wenn die Dreiecke \(\triangle ABF\) und \(\triangle CEF\) ähnlich sind. Und sie sind z.B. dann ähnlich, wenn sie in einem Winkel (also z.B. den bei \(F\)) und in einem Streckenverhältnis übereinstimen.

Die Winkel bei \(F\) sind Scheitelwinkel und folglich gleich. Wenn man davon ausgeht, dass beide Dreiecke gleichschenklich sind, ist auch eine zweite Bedingung für die Ähnlichkeit erfüllt. Auf die Gleichschenklichkeit lässt sich wegen der Symmetrie schließen: \(|FE| = |FC|\) und \(|FA|=|FB|\)

Wenn man aber die Symmetrie voraussetzt, ist es einfacher, eine Symmetrieachse \(DF\) bzw. \(DM\) - \(M\) ist die Mitte von \(AB\) - einzuführen. Dann bilden sich der Punkt \(E\) auf \(C\) und \(A\) auf \(B\) ab. Folglich stehen \(EC\) und \(AB\) beide senkrecht auf der Symmetrieachse und sind folglich parallel.