Wie viele Einheiten der primären Ressourcen sind nötig?

Question

Aufgabe:

Ein Unternehmen stellt drei Produkte A, B und C her. Dabei fallen Kosten für Arbeit (a), Energie (e), sowie für zwei Rohstoffe (r, s) an. Wir nehmen an, dass jeweils lineare Zusammenhänge bestehen; um die doppelte Menge von Produkt A herzustellen, ist also doppelt soviel Energie nötig wie für die einfache Menge usw. Eine andere Firma verwendet die Produkte A, B,C als Zwischenprodukte zur Herstellung von drei Endprodukten Odil (in Tuben), Xio (in Flaschen) und Tanx (in Dosen). Die Zusammenhänge werden in Verbrauchsmatrizen beschrieben:

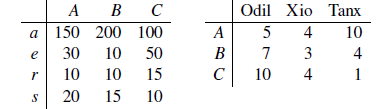
Wie viele Einheiten an den primären Ressourcen a, e, r, s sind notwendig, um 100 Tuben Odil, 200 Flaschen Xio und 150 Dosen Tanx herzustellen? Hinweis: Die durch die Verbrauchsmatrizen beschriebenen linearen Abbildungen laufen „entgegengesetzt“ zur Produktionsrichtung.

Problem/Ansatz:

Könnte mir jemand evtl helfen, komme hier leider gar nicht weiter

Answer 1

$$\left[\begin{array}{ccc}150 & 200 & 100 \\ 30 & 10 & 50 \\ 10 & 10 & 15 \\ 20 & 15 & 10\end{array}\right] \cdot\left[\begin{array}{ccc}5 & 4 & 10 \\ 7 & 3 & 4 \\ 10 & 4 & 1\end{array}\right] \cdot\left[\begin{array}{c}100 \\ 200 \\ 150\end{array}\right]=\left[\begin{array}{r}995000 \\ 200500 \\ 76250 \\ 104000\end{array}\right]$$