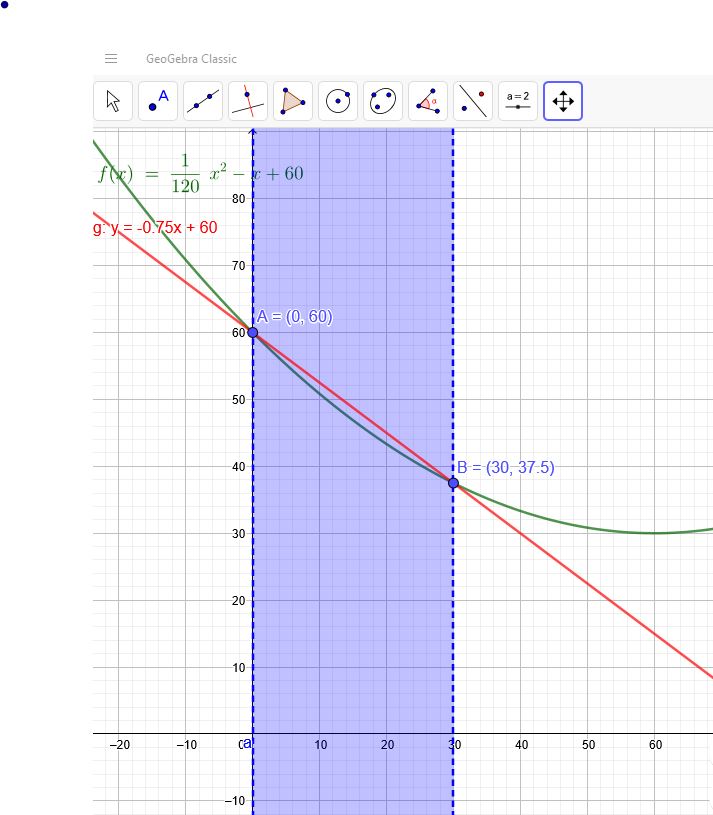
\(f(x)= \frac{1}{120} x^2 -x +60 (0 < x <30)\)
mittlere Steigung: \( \frac{f(30)-f(0)}{30-0} \)
\(f(30)= \frac{1}{120} * 30^2 -30 +60=\frac{75}{2}\)
\(f(0)= \frac{1}{120} * 0^2 -0 +60=60 \)
mittlere Steigung: \( \frac{\frac{75}{2}-60}{30}=-\frac{3}{4} \)