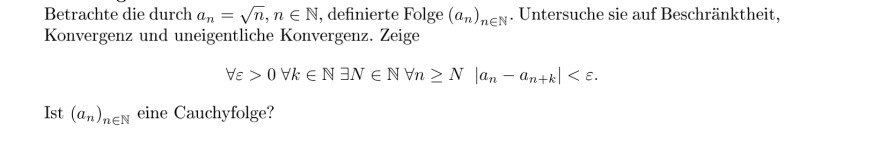
Text erkannt:
Betrachte die durch \( a_{n}=\sqrt{n}, n \in \mathbb{N} \), definierte Folge \( \left(a_{n}\right)_{n \in \mathbb{N}} \). Untersuche sie auf Beschränktheit, Konvergenz und uneigentliche Konvergenz. Zeige
\( \forall \varepsilon>0 \forall k \in \mathbb{N} \exists N \in \mathbb{N} \forall n \geq N\left|a_{n}-a_{n+k}\right|<\varepsilon \)
Ist \( \left(a_{n}\right)_{n \in \mathbb{N}} \) eine Cauchyfolge?