Aufgabe: Lösen einer Dgl mit geeigneter Substitution
Problem/Ansatz:
Hallo,
ich habe folgende Dgl. (Unten im Bild)
Ich habe meinen Ansatz unten einmal beigefügt.
Ich wollte im letzten Schritt die Dgl mit Tdv Integrieren, habe es jedoch nicht hinbekommen..
Sieht jemand einen fehler oder kann mir einen Lösungweg vorrechnen ??
Vielen Dank Leute!!
Gruß Frost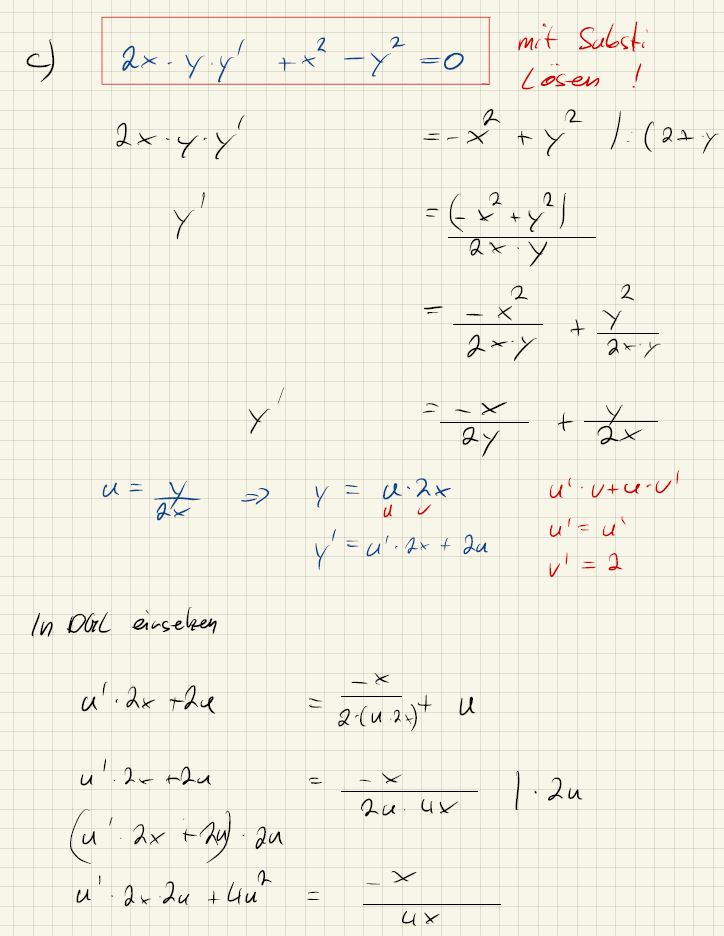
Text erkannt:
c) \( 2 x \cdot y \cdot y^{\prime}+x^{2}-y^{2}=0 \quad \) mit Substi
\( \begin{array}{l} \left.2 x \cdot y \cdot y^{\prime} \quad=-x^{2}+y^{2}\right):(2+y \\ y^{\prime} \quad=\frac{\left(-x^{2}+y^{2}\right)}{2 x \cdot y} \\ =\frac{-x^{2}}{2 x \cdot y}+\frac{y^{2}}{2 x \cdot y} \\ y^{\prime} \quad=\frac{-x}{2 y}+\frac{y}{2 x} \\ u=\frac{y}{2 x} \quad \Rightarrow \quad y=u \cdot 2 x \quad u^{\prime} \cdot v+u \cdot v^{\prime} \\ \begin{array}{ll} y^{\prime}=u^{\prime} \cdot 2 x+2 u & u^{\prime}=u^{\prime} \\ v^{\prime}=2 \end{array} \\ \end{array} \)
In Dorl eirseben
\( \begin{array}{l} u^{\prime} \cdot 2 x+2 u=\frac{-x}{2 \cdot(u \cdot 2 x}+u \\ u^{\prime} \cdot 2 x+2 u=\frac{-x}{2 u \cdot u x} \mid \cdot 2 u \\ \left(u^{\prime} \cdot 2 x+2 u\right) \cdot 2 u \\ u^{\prime} \cdot 2 x \cdot 2 u+4 u^{2}=\frac{-x}{u x} \end{array} \)

Text erkannt:
\( \begin{array}{rl} u^{\prime} \cdot 2 x \cdot 2 u & =-\frac{1}{4}-4 u^{2} \mid: 2 x \\ u^{\prime} \cdot 2 u & =\frac{-0.25}{2 x}-4 u^{2} \\ \frac{d u}{d x} \cdot 2 u & =\frac{-0,25}{2 x}-\frac{4 u^{2}}{2 x} \\ 2 & ? ? \end{array} \)
Bereduen Sie die allgemeine Losseng!