Aufgabe:
Text erkannt:
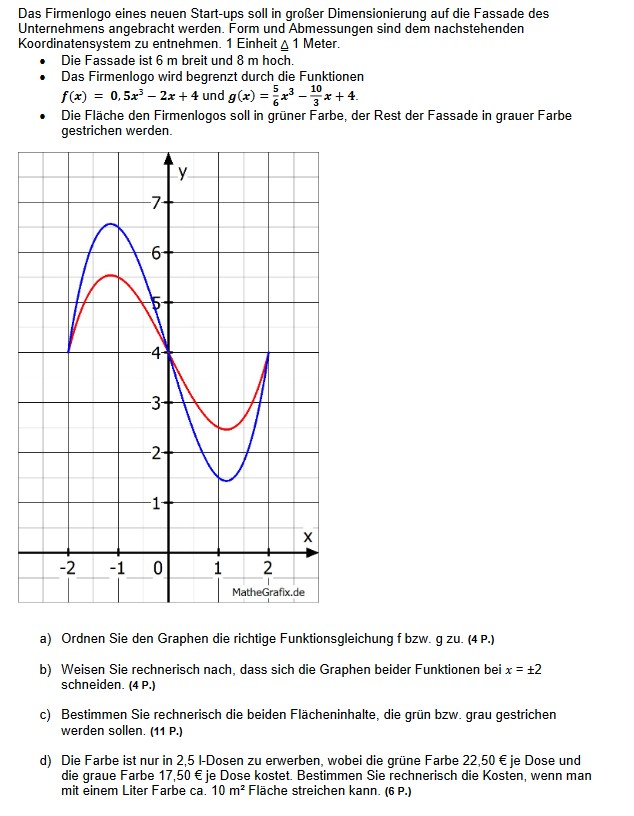
Das Firmenlogo eines neuen Start-ups soll in großer Dimensionierung auf die Fassade des Unternehmens angebracht werden. Form und Abmessungen sind dem nachstehenden Koordinatensystem zu entnehmen. 1 Einheit \( \triangleq 1 \) Meter.
- Die Fassade ist \( 6 \mathrm{~m} \) breit und \( 8 \mathrm{~m} \) hoch.
- Das Firmenlogo wird begrenzt durch die Funktionen \( f(x)=0,5 x^{3}-2 x+4 \) und \( g(x)=\frac{5}{6} x^{3}-\frac{10}{3} x+4 \)
- Die Fläche den Firmenlogos soll in grüner Farbe, der Rest der Fassade in grauer Farbe gestrichen werden.
a) Ordnen Sie den Graphen die richtige Funktionsgleichung f bzw. g zu. (4 P.)
b) Weisen Sie rechnerisch nach, dass sich die Graphen beider Funktionen bei \( x=\pm 2 \) schneiden. (4 P.)
c) Bestimmen Sie rechnerisch die beiden Flächeninhalte, die grün bzw. grau gestrichen werden sollen. (11 P.)
d) Die Farbe ist nur in 2,5 I-Dosen zu erwerben, wobei die grüne Farbe 22,50€ je Dose und die graue Farbe 17,50 € je Dose kostet. Bestimmen Sie rechnerisch die Kosten, wenn man mit einem Liter Farbe ca. 10 m \( ^{2} \) Fläche streichen kann. (6 P.)
Problem/Ansatz:
Die Aufgaben a), b) und c) habe ich so weit alle lösen können. Ich komme auf 2 2/3 m^2 Fläche, die gestrichen werden müssen. Woran ich nun zweifele ist die Aufgabe d). Mein Ansatz wäre hier - da die Dosen jeweils für 10m^2 ausreichen und immer in 2,5L-Form gekauft werden müssen - das ich ganz reinfach rechnen kann 6 * 8 - 2,666 / 10 => 5 * 17,50 (graue Farbe) und dann noch einmal 22,50€für die grüne Farbe. Also insgesamt 110€. Jedoch machen mich die 6 Punkte für eine derartige Aufgabe stutzig, übersehe ich hier etwas Versteckes?