
Text erkannt:
Ü 7.6.8 Eine Maschine besteht aus den drei Aggregaten A, B und C, die unabhängig voneinander mit den Wahrscheinlichkeiten \( \mathbf{P}(\mathrm{A})=0,3 ; \mathbf{P}(\mathrm{B})=0,2 \) und \( \mathbf{P}(\mathrm{C})=0,1 \) ausfallen. Die Maschine kann nur genutzt werden, wenn kein Einzelaggregat ausfällt.
Wie hoch ist die Wahrscheinlichkeit für den Ausfall der Maschine?
Wieso wird hier für das Ergebnis das komplementärereignis genutzt ?
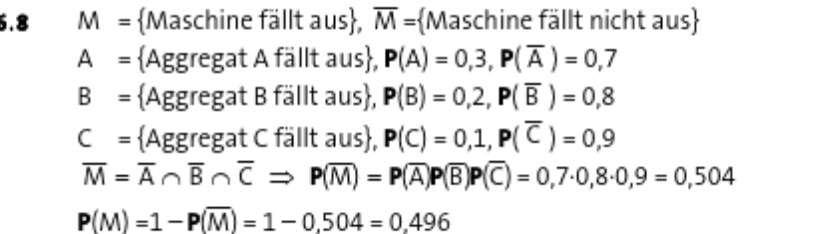
Text erkannt:
5.8 \( M=\{ \) Maschine fällt aus \( \}, \bar{M}=\{ \) Maschine fällt nicht aus \( \} \)
\( A=\{ \) Aggregat \( A \) fällt aus \( \}, \mathbf{P}(A)=0,3, \mathbf{P}(\bar{A})=0,7 \)
\( B=\{ \) Aggregat \( B \) fällt aus \( \}, \mathbf{P}(B)=0,2, \mathbf{P}(\bar{B})=0,8 \)
\( C=\{ \) Aggregat \( C \) fällt aus \( \}, P(C)=0,1, \mathbf{P}(\bar{C})=0,9 \)
\( \bar{M}=\bar{A} \cap \bar{B} \cap \bar{C} \Rightarrow \mathbf{P}(\bar{M})=\mathbf{P}(\bar{A}) \mathbf{P}(\bar{B}) \mathbf{P}(\bar{C})=0,7 \cdot 0,8 \cdot 0,9=0,504 \)
\( \mathbf{P}(M)=1-\mathbf{P}(\bar{M})=1-0,504=0,496 \)
kann man nicht gleich alle Wahrscheinlichkeiten dafür, dass es funktioniert multiplizieren ?