Aufgabe:
Setzt man einen Chip auf eine Zahl und diese wird getroffen, so bekommt man 36 Chips von der
Spielbank zurück. Bei 2 Zahlen sind es dann 18.
Kommentieren Sie die Aussage: Die Spielbank gewinnt „auf Dauer“ immer.
Problem/Ansatz:
Moin Leute ich habe Fragen zur Folgende Aufgabe.
1.) Ich weiß dass es 38 Felder gibt von 1-36 wenn ich die 0 und 00 dazu zähle (also wahrscheinlichkeit für eine Zahl 1/38) , doch leider kann nicht nachvollziehen warum ich wenn ich auf einer Zahl setze 36 chips zurück bekomme und bei 2 Zahlen 18 chips? Warum ist dies so ? Leider verstehe ich überhaupt Glückspiel nicht.
2.) Leider stehe ich bei der Aussage: Kommentieren Sie die Aussage: Die Spielbank gewinnt „auf Dauer“ immer. total aufn Schlauch. Ich meine was soll hier genau machen den Erwartungswert berechnen ?
Ich freue mich auf eure Hilfe :)
Text erkannt:
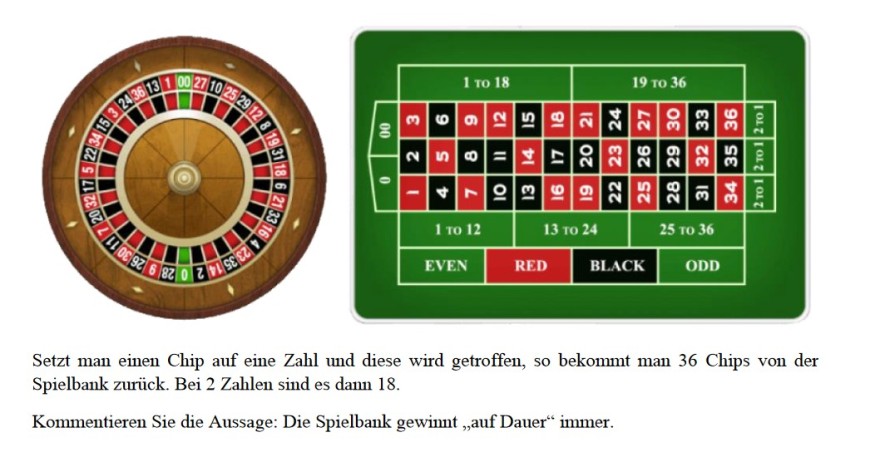
Setzt man einen Chip auf eine Zahl und diese wird getroffen, so bekommt man 36 Chips von der Spielbank zurück. Bei 2 Zahlen sind es dann 18.
Kommentieren Sie die Aussage: Die Spielbank gewinnt ,auf Dauer“ immer.