Aufgabe:
Haldelt es sich um Flächenparametrisierungen?
Problem/Ansatz:
Damit eine vektorielle Funktion als eine Flächenparametrisierung bezeichnet werden kann, muss es folgendes erfüllen:
I das Kreuzprodukt der partiellen Ableitungen darf nicht gleich Null sein UND
II die einzelnen Komponenten müssen injektive Funktionen sein.
Angabe: Winkel mit (0,2pi) und z mit (0, infinity).
Bei der folgenden Funktion (unteres Bspl) soll es sich auch um eine Flächenparametrisierung handeln, ich verstehe aber nicht, wie sie denn injektiv sein könnte? Es ist ja sinus und cosinus im Intervall (0,2pi).
Danke und lg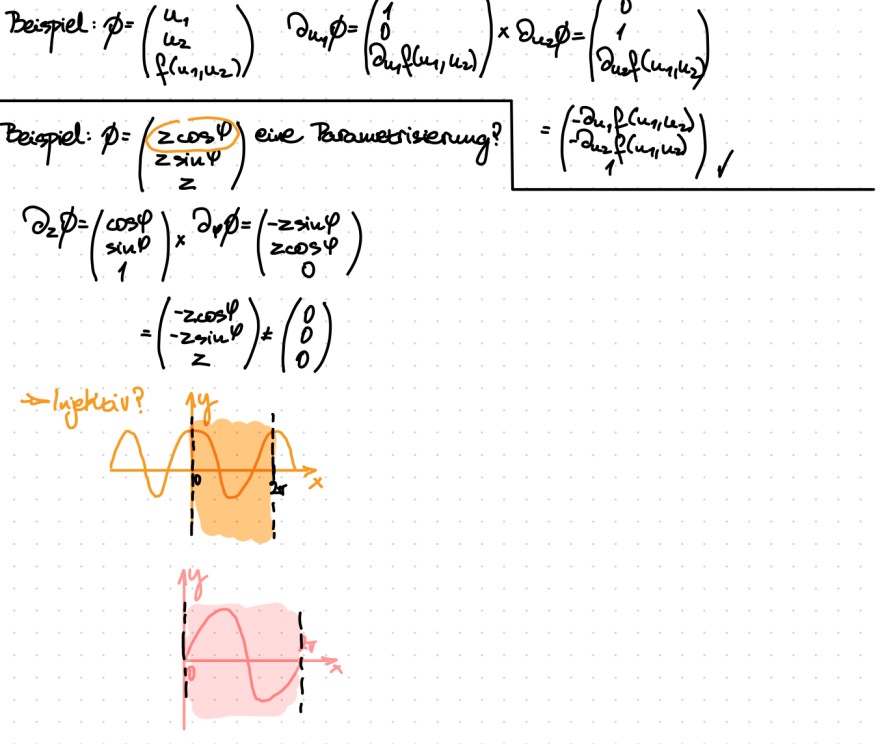
Text erkannt:
\( \begin{array}{l} \text { Beispiel: } \phi=\left(\begin{array}{l} u_{1} \\ u_{2} \\ f\left(u_{1}, u_{2}\right) \end{array}\right) \quad \partial_{u_{1}} \phi=\left(\begin{array}{c} 1 \\ 0 \\ \partial_{u_{1}} f\left(u_{1}, u_{2}\right) \end{array}\right) \times \partial_{u_{2}} \phi=\left(\begin{array}{c} 0 \\ 1 \\ \partial_{u_{2} f}\left(u_{1}, u_{2}\right) \end{array}\right) \\ \text { Beispiel: } \phi=\left(\begin{array}{rl} 2 \cos \varphi \\ 2 \sin \varphi \\ z \end{array}\right) \text { eine Parametriserung? }=\left(\begin{array}{c} -\partial_{u_{1}} f\left(u_{1} u_{2}\right) \\ \partial_{u_{2}} f\left(u_{1} u_{2}\right) \\ 1 \end{array}\right) \\ \partial_{2} \phi=\left(\begin{array}{c} \cos \varphi \\ \sin \varphi \\ 1 \end{array}\right) \times \partial_{\varphi} \phi=\left(\begin{array}{c} -2 \sin \varphi \\ 2 \cos \varphi \\ 0 \end{array}\right) \\ =\left(\begin{array}{c} -2 \cos \varphi \\ -2 \sin \varphi \\ z \end{array}\right) \neq\left(\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right) \end{array} \)
- Injektiv?