Aufgabe:
Text erkannt:
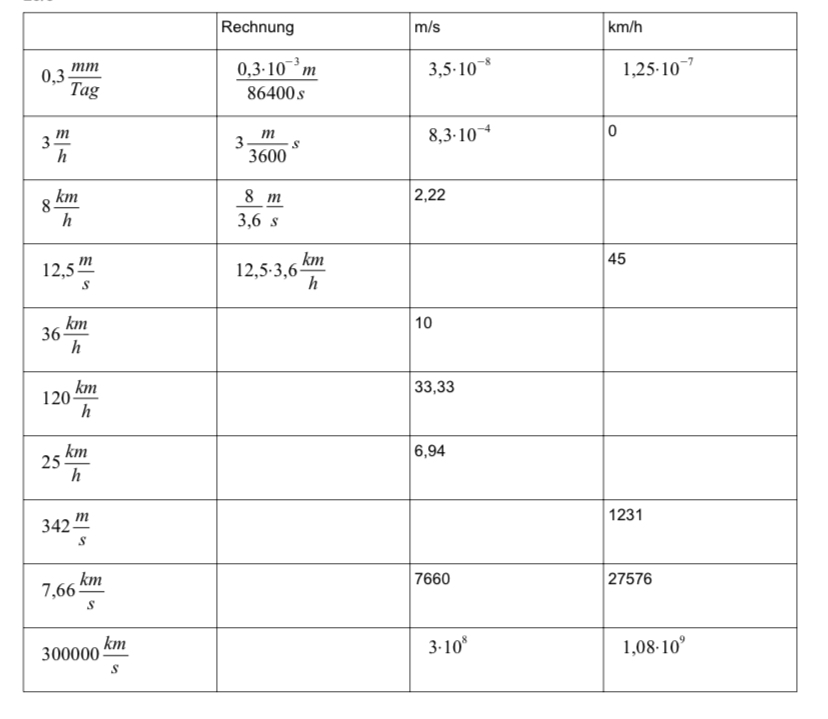
\begin{tabular}{|l|l|l|l|}
\hline & Rechnung & \( \mathrm{m} / \mathrm{s} \) & \( \mathrm{km} / \mathrm{h} \) \\
\hline \( 0,3 \frac{\mathrm{mm}}{\mathrm{Tag}} \) & \( \frac{0,3 \cdot 10^{-3} \mathrm{~m}}{86400 \mathrm{~s}} \) & \( 3,5 \cdot 10^{-8} \) & \( 1,25 \cdot 10^{-7} \) \\
\hline \( 3 \frac{\mathrm{m}}{\mathrm{h}} \) & \( 3 \frac{\mathrm{m}}{3600} \mathrm{~s} \) & \( 8,3 \cdot 10^{-4} \) & 0 \\
\hline \( 8 \frac{\mathrm{km}}{\mathrm{h}} \) & \( \frac{8}{3,6} \frac{\mathrm{m}}{\mathrm{s}} \) & 2,22 & \\
\hline \( 12,5 \frac{\mathrm{m}}{\mathrm{s}} \) & \( 12,5 \cdot 3,6 \frac{\mathrm{km}}{\mathrm{h}} \) & 10 & \\
\hline \( 36 \frac{\mathrm{km}}{\mathrm{h}} \) & & 35 & \\
\hline \( 120 \frac{\mathrm{km}}{\mathrm{h}} \) & & 3,33 & \\
\hline \( 25 \frac{\mathrm{km}}{\mathrm{h}} \) & & 3660 & \\
\hline \( 342 \frac{\mathrm{m}}{\mathrm{s}} \) & & & \\
\hline \( 7,66 \frac{\mathrm{km}}{\mathrm{s}} \) & & & \\
\hline \( 300000 \frac{\mathrm{km}}{\mathrm{s}} \) & & & \\
\hline
\end{tabular}
…
Problem/Ansatz:
Ich verstehe nicht ganz, wie man beim ersten auf die Lösung kommt. Vonwo weiß ich nämlich dass ich mal 10^-3 rechnen muss und woher die 86400 aufeinmal her kommt.
Beim zweiten verstehe ich nicht, warum ich die 3 vor den Bruch machen muss und wie ich das dann ausrechne, wenn m fehlt.
Und beim letzen wollte ich wissen, wie man auf das Ergebnis kommt, also wie man da rechnen muss.