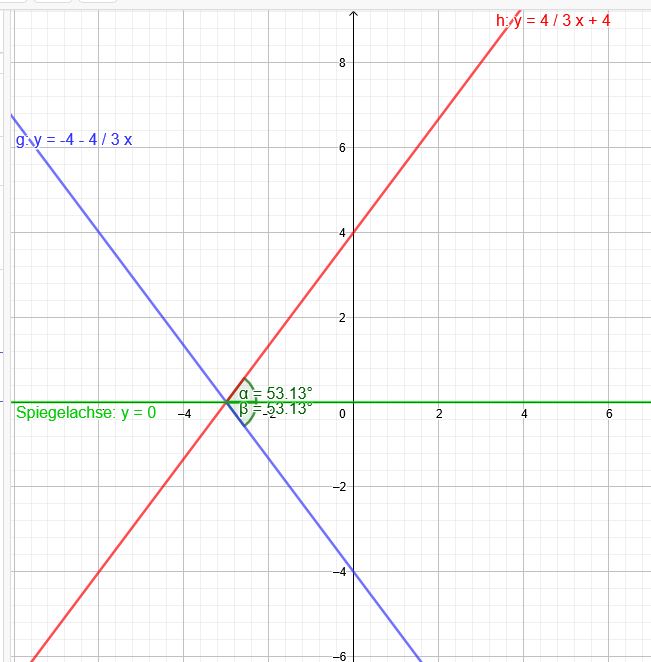
h: \( y=\frac{4}{3} x+4 \)
Gerade auf dem Bild:
Mit der Achsenabschnittsform: g: \( \frac{x}{-3}+\frac{y}{-4}=1 \)
\(\frac{y}{-4}=1-\frac{x}{-3} \) → \(\frac{y}{-4}=1+\frac{x}{3} \) → \(y=-4-\frac{4}{3}x \)
Schnittpunkt beider Geraden:
\(-4-\frac{4}{3}x=\frac{4}{3} x+4\)
\(-\frac{4}{3}x=\frac{4}{3} x+8\)
\(-\frac{4}{3}x-\frac{4}{3} x=8\)
\(-\frac{8}{3}x=8\)
\(x=-3\) \( y(-3)=\frac{4}{3} *(-3)+4=0 \)
\(N(-3|0)\)
Winkel zwischen \( y=\frac{4}{3} x+4 \) und der x-Achse:
\(\tan(\alpha)=\frac{4}{3} \Rightarrow \alpha=53,13°\)
Winkel zwischen \( y=-\frac{4}{3} x-4 \) und der x-Achse:
\(\tan(β)=-\frac{4}{3} \) \(\Rightarrow β=-53,13°\)
Somit ist die Gerade h das Bild der Geraden g nach Spiegelung an der x-Achse.