Aufgabe:
Text erkannt:
\begin{tabular}{c|c|c|c|c}
\( x \) & \( -2 \) & 2 & 0 & \( -4 \) \\
\hline\( f(x) \) & 4 & 8 & 10 & \( -10 \)
\end{tabular}
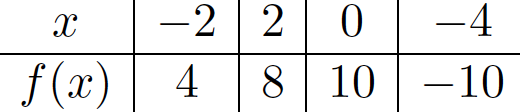
Berechnen Sie das das Interpolationspolynom zu folgenden Stellen und Werte
1. bestimmen der Koeffizienten aᴶ für
Text erkannt:
\( p_{n}(x)=\sum \limits_{j=0}^{n} a_{j} x^{j} \)
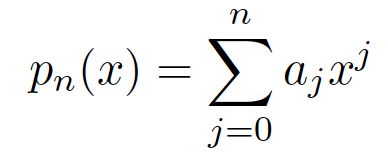
mithilfe der Vandermonde Matrix
2. bestimmen der Koeffizienten f(xᴶ) und der Polynome Lᴶᴺ für:
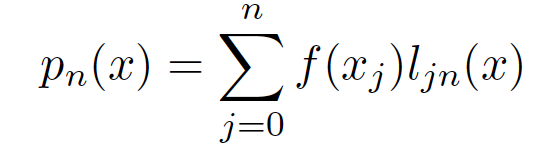
Text erkannt:
\( p_{n}(x)=\sum \limits_{j=0}^{n} f\left(x_{j}\right) l_{j n}(x) \)
3. Werten Sie das Polynom für x = 4 und x = 7 aus
Problem/Ansatz: Ich habe bei der 1. die Werte in die Gleichung p(x) = a0+a1x+a2x²+a3x³ eingesetzt und die entsprechende Vandermonde Matrix gebildet. Allerdings kam als Lösung der Matrix / Gleichungssystems das Ergebnis: ,,keine Lösung" heraus und ich weiß ab hier nicht mehr weiter.
Ich habe für:
p(-2) = a0-2a1-4a2-8a3; p(2) = a0+2a1+4a2+8a3; p(0) = a0; p(-4) = a0-4a1-16a2-64a3 ist das korrekt und wenn ja wo liegt dann mein Fehler.
Bei 2. und 3. kann ich nicht weitermachen solange ich die 1 nicht gelöst habe.
Danke schonmal im Voraus :)