Aufgabe: Geben Sie für folgende Mengen die inneren Punkte sowie die Randpunkte an, und entscheiden Sie, ob die jeweilige Menge offen ist:
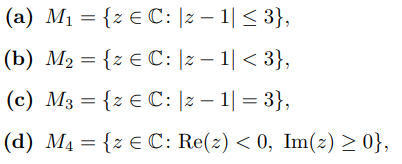
Text erkannt:
(a) \( M_{1}=\{z \in \mathbb{C}:|z-1| \leq 3\} \),
(b) \( M_{2}=\{z \in \mathbb{C}:|z-1|<3\} \),
(c) \( M_{3}=\{z \in \mathbb{C}:|z-1|=3\} \),
(d) \( M_{4}=\{z \in \mathbb{C}: \operatorname{Re}(z)<0, \operatorname{Im}(z) \geq 0\} \)
Problem/Ansatz:
Leider hab ich überhaupt keinen Plan (man findet im Internet leider auch keine hilfreichen Erklärungen).